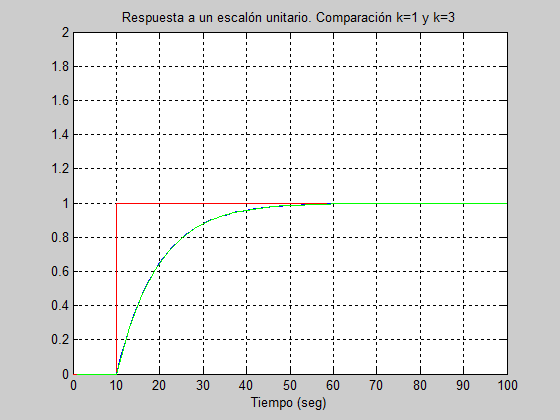
Matlab - Representar función discreta como continua

Hola a todos

Tengo un problema básicamente, y es que no tengo base de control adaptativo y mis conocimientos de Matlab son muy básicos y son adquiridos de forma autónoma.

Dicho esto, necesito demostrar que dos funciones representan al mismo proceso, una con un periodo de control de 1s y otra con un periodo de control de 3s. Es condición del problema que se haga la simulación del proceso mediante un bucle for.

A la hora de representarlas, no tengo ningún problema con la de 1s, pero soy incapaz de obtener una representación análoga para la de 3s, ya que los periodos que me salto me los considera 0 y me hace los siguiente:



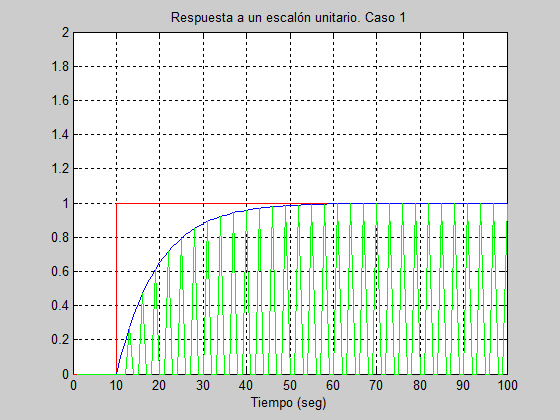
Incluyo el código. Los factores del principio, a1 y b1 son del enunciado, y a3 y b3 son calculados para el periodo de control 3s, y parecen correctos a la vista de la gráfica.

a1=0.9;
b1=0.1;
a3=0.729;
b3=0.271;
u = zeros(1,100);
y1 = zeros(1,100);
y3 = zeros(1,100);
for k1=1:100;
if k1>=10;
u(k1) = 1;
elseif k1<=10;
u(k1) =0;
end
if k1<=10;
y1(k1) = 0;
else
y1(k1) = a1*y1(k1-1)+b1*u(k1-1);
end
fprintf('Valor de la entrada en k = %i : u(%i) = %i\n',k1,k1,u(k1));
fprintf('Valor de la salida en k = %i : y(%i) = %i\n',k1,k1,y1(k1));
v1(k1)=k1;
end
for k=1:34;
k3=1+3*(k-1);
v(k) = k3;
if k3>=10;
u(k3) = 1;
else;
u(k3) =0;
end
if k3<=10;
y3(k3) = 0;
else
y3(k3) = a3*y3(k3-3)+b3*u(k3-3);
v2(k) = y3(k3);
if v2(k)==0;
v2(k)=[];
end
end

fprintf('Valor de la entrada en k = %i : u(%i) = %i\n',k3,k3,u(k3));
fprintf('Valor de la salida en k = %i : y(%i) = %i\n',k3,k3,y3(k3));

end
u=[zeros(1,10000),ones(1,90001)];
t=0:.001:100;
plot(t,u,'r');
hold on;

plot (y1);

%y3=[v;v2]';

plot (y3,'g');
axis ([0 100 0 2]);
title ('Respuesta a un escalón unitario. Caso 1');
xlabel ('Tiempo (seg)');
grid;
hold off;

Como podréis comprobar, también tuve que hacer un apaño para que la señal escalón unitario me aparezca representada como tal, ya que era incapaz de conseguir el tramo vertical.

Espero que me podáis ayudar.

Muchas gracias

Estoy revisando tu código,
Podrias detallar lo que deseas, para poder contestarte con mas certeza.


debe ser excluyente esta parte:

Buenas José Jeremías

El problema lo tengo en la función y3, del segundo bucle. En el código que pongo en el primer mensaje incluyo los dos para que se vea que en un caso funciona y en otro no. La diferencia entre y1 e y3 es que en el primer caso tomo valores cada 1 segundo y en y3 tomo valores cada 3 segundos, con lo cual la ecuación del proceso cambia.

Conseguí "arreglarlo" generando dos vectores v y v2, en los que v toma los valores de k3 (puntos del eje x en que la función y3 toma valores) y v2 son los valores de y3 en dichos momentos.

El segundo bucle me queda así:


A pesar de que los valores de k3 aumentan como quiero (1,4,7,10...) la función y3 considera también los puntos intermedios y les da valor cero, de ahí que me saliese la gráfica dentada en verde del primer post.
Al generar el vector v2, le elimino los términos que valgan cero y me quedo así con los que quiero. Así tengo la representación, sustituyendo y3 por v (valores en x) y v2 (valores en y). El código representa el escalón unitario (en rojo), la función para el periodo de control 1s (en azul) y 3s (en verde), estas dos últimas casi superpuestas:


El resultado:



No sé si es un método muy académico, pero al menos me sacó del atolladero.

Un saludo.