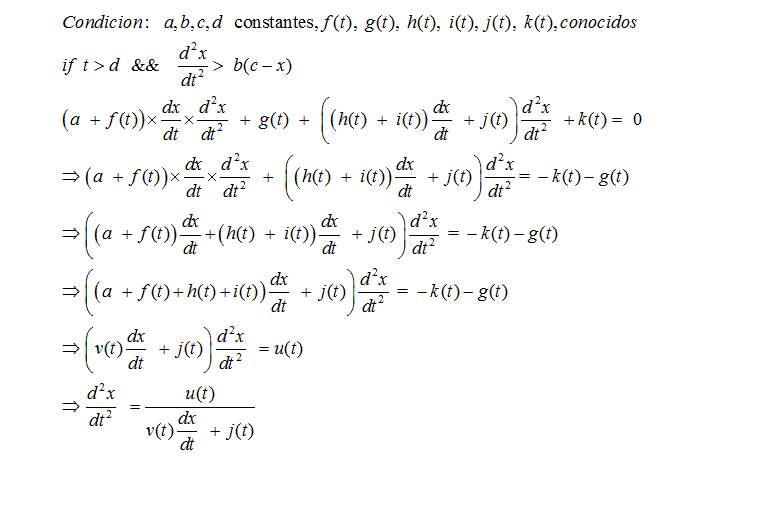Resolución EDO 2o orden con inecuación interna - Matlab
Publicado por Jaime (3 intervenciones) el 10/05/2017 20:23:38
Tengo esta EDO de 2o orden para resolver en Matlab:
(a + f(t))·(dx/dt)·(d²x/dt²) + g(t) + ((h(t) + i(t)·(d²x/dt² > b·(c-x)))·(dx/dt) + j(t))·(dx/dt)² + k(t)·(t > d) = 0
donde
- `a`,`b`,`c`,`d` son constantes conocidas
- `f(t)`,`g(t)`,`h(t)`,`i(t)`,`j(t)`,`k(t)` son funciones conocidas dependientes del parámetro `t`
- `x` es la posici'on
- `dx/dt` es la velocidad
- `d²x/dt²` es la aceleracion
y nótese las dos condiciones introducidas:
- `i(t)` aparece en la ecuación si `(d²x/dt² > b·(c-x))`
- `k(t)` aparece en la ecuación si `(t > d)`
Así, el problema puede resolverse con la siguiente estructura en Matlab como ejemplo:
[T,Y] = ode45(@(t,y) [y(2); 'Expressión de la aceleración DESCONOCIDA'], tspan, [x0 v0]);
donde
- `T` es el vector tiempo, `Y` es el vector posición (columna 1 como `y(1)`) y velocidad (columna 2 como `y(2)`).
- `ode45` es el ODE solver, pero se puede usar cualquier otro.
- `tspan`,`x0`,`v0` son conocidos y constantes
- `Expressión de la aceleración DESCONOCIDA` significa la expresión para `d²x/dt²`, pero **aquí viene el problema, puesto que está dentro de la condición para `i(t)` y 'fuera' al mismo tiempo multiplicnado a `(a + f(t))·(dx/dt)`**. Así, a priori la aceleración no puede escribirse como en Matlab`d²x/dt² = algo` y aquí es donde os necesito.
Algunas cosas que pueden ayudar:
- Una vez que la condicion `(d²x/dt² > b·(c-x))` y/o `(t > d)` se satisface, el término respectivo `i(t)` y/o `k(t)` será introducido hasta el final del determinado tiempo `tspan`.
- Para la condicion `(d²x/dt² > b·(c-x))`, el término `d²x/dt²` podría escribirse como la diferencia de velocidades, como `y(2) - y(2)'`, si `y(2)'` es la velocidad del instante anterior, dividida entre el step-time defined in `tspan`. Sin embargo, no sé **cómo acceder al valor previo de la velocidad _durante_ la resolución de la EDO**
Muchas gracias en adelanto !
(a + f(t))·(dx/dt)·(d²x/dt²) + g(t) + ((h(t) + i(t)·(d²x/dt² > b·(c-x)))·(dx/dt) + j(t))·(dx/dt)² + k(t)·(t > d) = 0
donde
- `a`,`b`,`c`,`d` son constantes conocidas
- `f(t)`,`g(t)`,`h(t)`,`i(t)`,`j(t)`,`k(t)` son funciones conocidas dependientes del parámetro `t`
- `x` es la posici'on
- `dx/dt` es la velocidad
- `d²x/dt²` es la aceleracion
y nótese las dos condiciones introducidas:
- `i(t)` aparece en la ecuación si `(d²x/dt² > b·(c-x))`
- `k(t)` aparece en la ecuación si `(t > d)`
Así, el problema puede resolverse con la siguiente estructura en Matlab como ejemplo:
[T,Y] = ode45(@(t,y) [y(2); 'Expressión de la aceleración DESCONOCIDA'], tspan, [x0 v0]);
donde
- `T` es el vector tiempo, `Y` es el vector posición (columna 1 como `y(1)`) y velocidad (columna 2 como `y(2)`).
- `ode45` es el ODE solver, pero se puede usar cualquier otro.
- `tspan`,`x0`,`v0` son conocidos y constantes
- `Expressión de la aceleración DESCONOCIDA` significa la expresión para `d²x/dt²`, pero **aquí viene el problema, puesto que está dentro de la condición para `i(t)` y 'fuera' al mismo tiempo multiplicnado a `(a + f(t))·(dx/dt)`**. Así, a priori la aceleración no puede escribirse como en Matlab`d²x/dt² = algo` y aquí es donde os necesito.
Algunas cosas que pueden ayudar:
- Una vez que la condicion `(d²x/dt² > b·(c-x))` y/o `(t > d)` se satisface, el término respectivo `i(t)` y/o `k(t)` será introducido hasta el final del determinado tiempo `tspan`.
- Para la condicion `(d²x/dt² > b·(c-x))`, el término `d²x/dt²` podría escribirse como la diferencia de velocidades, como `y(2) - y(2)'`, si `y(2)'` es la velocidad del instante anterior, dividida entre el step-time defined in `tspan`. Sin embargo, no sé **cómo acceder al valor previo de la velocidad _durante_ la resolución de la EDO**
Muchas gracias en adelanto !
Valora esta pregunta


0