
Completar una matriz usando el teorema del resto chino
Publicado por Agustín (1 intervención) el 24/02/2018 23:45:48
Hola gente,
El problema que no puedo resolver es el siguiente:
La idea es, teniendo un vector con N elementos, en donde N = m*n , poder completar una matriz (m,n) usando el teorema del resto chino .
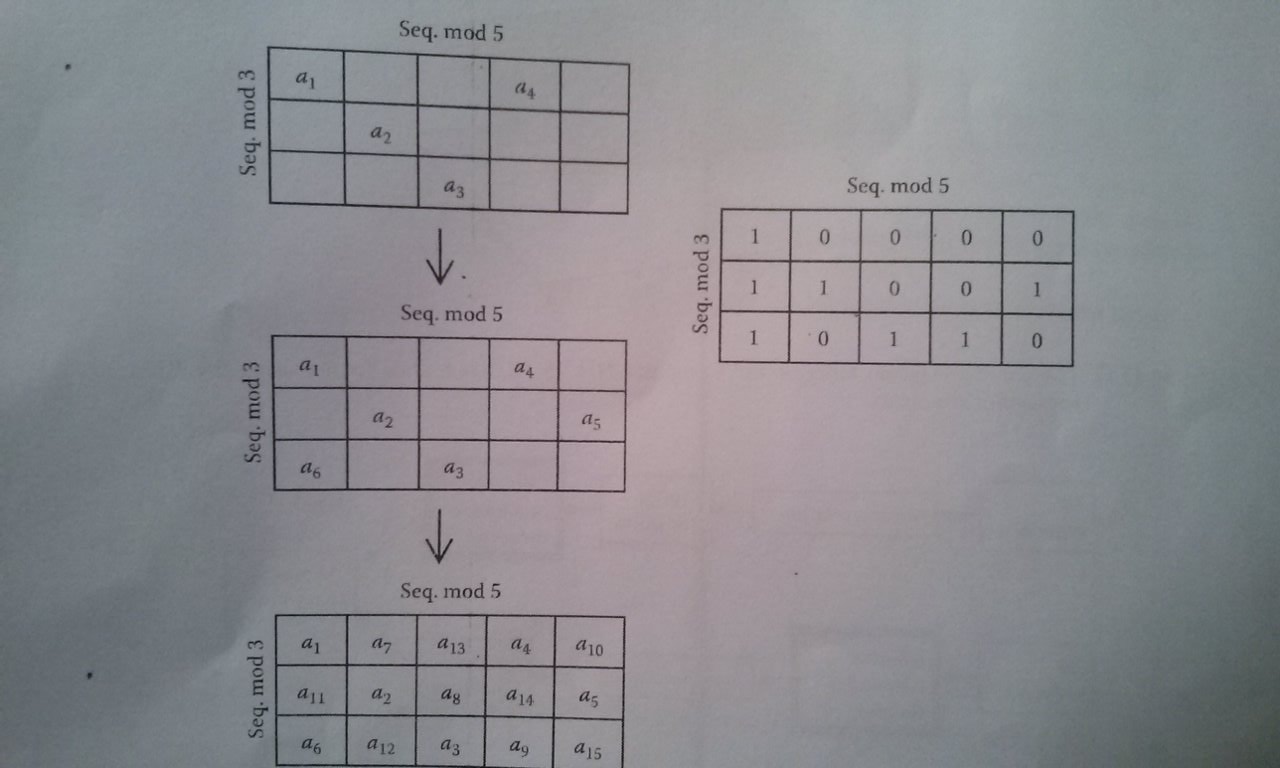
La secuencia a seguir la adjunto en una foto.
en el ejemplo se utiliza un vector de 15 elementos ( V= {1 1 1 0 1 1 0 0 1 0 1 0 0 0 0}) y una matriz de 3x5. Esto no siempre es así, ya que el vector es una secuencia MLS cuya longitud viene dada por N = 2^n - 1 (n = entero positivo), por lo que el tamaño de la matriz está condicionada a que la multiplicación de las filas por las columnas de como resultado algún N posible.
Espero que se haya entendido,
desde ya,muchas gracias.
El problema que no puedo resolver es el siguiente:
La idea es, teniendo un vector con N elementos, en donde N = m*n , poder completar una matriz (m,n) usando el teorema del resto chino .
La secuencia a seguir la adjunto en una foto.
en el ejemplo se utiliza un vector de 15 elementos ( V= {1 1 1 0 1 1 0 0 1 0 1 0 0 0 0}) y una matriz de 3x5. Esto no siempre es así, ya que el vector es una secuencia MLS cuya longitud viene dada por N = 2^n - 1 (n = entero positivo), por lo que el tamaño de la matriz está condicionada a que la multiplicación de las filas por las columnas de como resultado algún N posible.
Espero que se haya entendido,
desde ya,muchas gracias.

Valora esta pregunta


0
