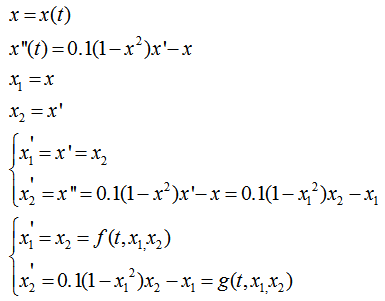runge kutta dos ecuaciones
Publicado por jose madriz (8 intervenciones) el 08/04/2018 12:35:55
Necesito una ayuda a como meter las funciones f y g. ya que me arroja error
las ecuaciones que quiero poner seria
dx/dt=x´
dx'/dt=0.1*(1-x^2)*x´-x
que es la de van der pol, ya que necesito gratificarla pero sin usar el comando
las ecuaciones que quiero poner seria
dx/dt=x´
dx'/dt=0.1*(1-x^2)*x´-x
que es la de van der pol, ya que necesito gratificarla pero sin usar el comando
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
%% runge kutta dos ecuaciones
x1=1y1=0h=0.05
t(1)=0;x(1)=x1;y(1)=y1
x(t)=x'
dx'=0.1*(1-x^2)*x'-x
f=j;g=dw;F=inline(f,'t','w','j');
G=inline(g,'t','w','j');
fprintf('%10.6f %10.6f %10.6f\n',t(1),w,j);
for i=1t(i+1)=t(1)+i*h
k(1)=h*F(t(i),x(i),y(i));
l(1)=h*G(t(i),x(i).y(i))
k(2)=h*F(t(i)+h/2,x(i)+k(1)/2,y(i)+l(1)/2);
l(2)=h*G(t(i)+h/2,x(i)+k(1)/2,y(i)+l(1)/2);
k(3)=h*F(t(i)+h/2,x(i)+k(2)/2,y(i)+l(2)/2);
l(3)=h*G(t(i)+h/2,x(i)+k(2)/2,y(i)+l(2)/2);
k(4)=h*F(t(i)+h,x(i)+k(3),y(i)+l(3));
l(4)=h*G(t(i)+h,x(i)+k(3),y(i)+l(3));
x(i+1)=x(i)+(1/6)*(k(1)+x*k(2)+x*k(3)+k(4));
y(i+1)=y(i)+(1/6)*(l(1)+2*l(2)+2*l(3)+l(4));
fprintf('%10.6f %10.6f %10.6f/n',t(i+1),x(i+1),y(i+1));
end
plot(t,x,'r-',t,y,'b-')
Valora esta pregunta


0