
Soy novat en python y no puedo correr un codigo en ANACONDA alguien podria ayudarme o explicarme?
Publicado por kami (1 intervención) el 03/06/2017 05:57:02
El código lo obtuve de esta pagina:
http://goelhardik.github.io/2016/10/04/fishers-lda/
-descargue e instale python 2.7
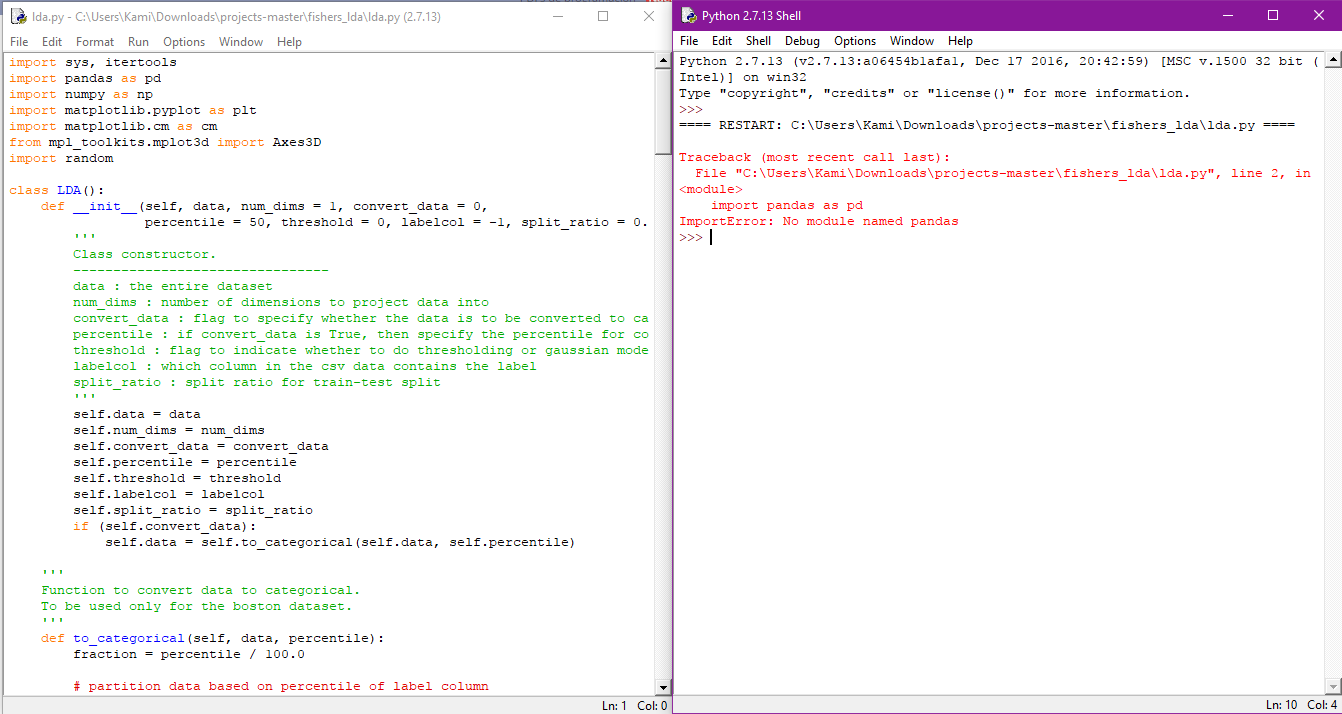
-lo primero que me apareció es que faltaba la libreria pandas, buscando en internet encontré en el sitio oficial que la forma mas facil de obtenerlo para windows era descargando anaconda xq ya lo tenia
-En fin no puedo y no se como hacerle para correr este programa
Algun@ de ustedes podrá ayudarme??
Pues necesito un ejemplo de programa FISHER LDA y ando mas que LOST
muchas gracias a tod@s por su amable atención
http://goelhardik.github.io/2016/10/04/fishers-lda/
-descargue e instale python 2.7
-lo primero que me apareció es que faltaba la libreria pandas, buscando en internet encontré en el sitio oficial que la forma mas facil de obtenerlo para windows era descargando anaconda xq ya lo tenia
-En fin no puedo y no se como hacerle para correr este programa
Algun@ de ustedes podrá ayudarme??
Pues necesito un ejemplo de programa FISHER LDA y ando mas que LOST
muchas gracias a tod@s por su amable atención
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
import sys, itertoolsimport pandas as pd
import numpy as np
import matplotlib.pyplot as pltimport matplotlib.cm as cmfrom mpl_toolkits.mplot3d import Axes3Dimport random
class LDA():
def __init__(self, data, num_dims = 1, convert_data = 0,
percentile = 50, threshold = 0, labelcol = -1, split_ratio = 0.9):
'''
Class constructor.
--------------------------------
data : the entire dataset
num_dims : number of dimensions to project data into
convert_data : flag to specify whether the data is to be converted to categorical
percentile : if convert_data is True, then specify the percentile for conversion
threshold : flag to indicate whether to do thresholding or gaussian modeling for classification
labelcol : which column in the csv data contains the label
split_ratio : split ratio for train-test split
'''
self.data = data
self.num_dims = num_dims
self.convert_data = convert_data
self.percentile = percentile
self.threshold = threshold
self.labelcol = labelcol
self.split_ratio = split_ratio
if (self.convert_data):
self.data = self.to_categorical(self.data, self.percentile)
'''
Function to convert data to categorical.
To be used only for the boston dataset.
'''
def to_categorical(self, data, percentile):
fraction = percentile / 100.0
# partition data based on percentile of label column
med = data.ix[:, self.labelcol].quantile(fraction)
for i in range(data.shape[0]):
if (data.ix[i, self.labelcol] >= med):
data.ix[i, self.labelcol] = 1
else:data.ix[i, self.labelcol] = 0
return data
'''
Utility function to drop some column from the given pandas dataframe.
'''
def drop_col(self, data, col):
return data.drop(data.columns[[col]], axis = 1)
'''
Main function to apply LDA
'''
def fit(self):
# Function estimates the LDA parameters
def estimate_params(data):
# group data by label column
grouped = data.groupby(self.data.ix[:,self.labelcol])
# calculate means for each class
means = {}
for c in self.classes:
means[c] = np.array(self.drop_col(self.classwise[c], self.labelcol).mean(axis = 0))
# calculate the overall mean of all the data
overall_mean = np.array(self.drop_col(data, self.labelcol).mean(axis = 0))
# calculate between class covariance matrix
# S_B = \sigma{N_i (m_i - m) (m_i - m).T}
S_B = np.zeros((data.shape[1] - 1, data.shape[1] - 1))
for c in means.keys():
S_B += np.multiply(len(self.classwise[c]),
np.outer((means[c] - overall_mean),
(means[c] - overall_mean)))
# calculate within class covariance matrix
# S_W = \sigma{S_i}
# S_i = \sigma{(x - m_i) (x - m_i).T}
S_W = np.zeros(S_B.shape)
for c in self.classes:
tmp = np.subtract(self.drop_col(self.classwise[c], self.labelcol).T, np.expand_dims(means[c], axis=1))
S_W = np.add(np.dot(tmp, tmp.T), S_W)
# objective : find eigenvalue, eigenvector pairs for inv(S_W).S_B
mat = np.dot(np.linalg.pinv(S_W), S_B)
eigvals, eigvecs = np.linalg.eig(mat)
eiglist = [(eigvals[i], eigvecs[:, i]) for i in range(len(eigvals))]
# sort the eigvals in decreasing order
eiglist = sorted(eiglist, key = lambda x : x[0], reverse = True)
# take the first num_dims eigvectors
w = np.array([eiglist[i][1] for i in range(self.num_dims)])
self.w = w
self.means = means
return
# perform train-test split
traindata = []
testdata = []
# group data by label column
grouped = data.groupby(self.data.ix[:,self.labelcol])
self.classes = [c for c in grouped.groups.keys()]
self.classwise = {}
for c in self.classes:
self.classwise[c] = grouped.get_group(c)
rows = random.sample(self.classwise[c].index,
int(self.classwise[c].shape[0] *
self.split_ratio))
traindata.append(self.classwise[c].ix[rows])
testdata.append(self.classwise[c].drop(rows))
traindata = pd.concat(traindata)
testdata = pd.concat(testdata)
# estimate the LDA parameters
estimate_params(traindata)
# perform classification on test set
# if the method is threshold
if (self.threshold):
self.calculate_threshold()
# append the training and test error rates for this iteration
trainerror = self.calculate_score(traindata) / float(traindata.shape[0])
testerror = self.calculate_score(testdata) / float(testdata.shape[0])
# if the method is gaussian modeling
else:self.gaussian_modeling()
# append the training and test error rates for this iteration
trainerror = self.calculate_score_gaussian(traindata) / float(traindata.shape[0])
testerror = self.calculate_score_gaussian(testdata) / float(testdata.shape[0])
return trainerror, testerror'''
Function to calculate the classification threshold.
Projects the means of the classes and takes their mean as the threshold.
Also specifies whether values greater than the threshold fall into class 1
or class 2.
'''
def calculate_threshold(self):
# project the means and take their mean
tot = 0for c in self.means.keys():
tot += np.dot(self.w, self.means[c])
self.w0 = 0.5 * tot
# for 2 classes case; mark if class 1 is >= w0 or < w0
c1 = self.means.keys()[0]
c2 = self.means.keys()[1]
mu1 = np.dot(self.w, self.means[c1])
if (mu1 >= self.w0):
self.c1 = 'ge'
else:self.c1 = 'l'
'''
Function to calculate the scores in thresholding method.
Assigns predictions based on the calculated threshold.
'''
def calculate_score(self, data):
inputs = self.drop_col(data, self.labelcol)
# project the inputs
proj = np.dot(self.w, inputs.T).T
# assign the predicted class
c1 = self.means.keys()[0]
c2 = self.means.keys()[1]
if (self.c1 == 'ge'):
proj = [c1 if proj[i] >= self.w0 else c2 for i in range(len(proj))]
else:proj = [c1 if proj[i] < self.w0 else c2 for i in range(len(proj))]
# calculate the number of errors made
errors = (proj != data.ix[:, self.labelcol])
return sum(errors)
'''
Function to estimate gaussian models for each class.
Estimates priors, means and covariances for each class.
'''
def gaussian_modeling(self):
self.priors = {}
self.gaussian_means = {}
self.gaussian_cov = {}
for c in self.means.keys():
inputs = self.drop_col(self.classwise[c], self.labelcol)
proj = np.dot(self.w, inputs.T).T
self.priors[c] = inputs.shape[0] / float(self.data.shape[0])
self.gaussian_means[c] = np.mean(proj, axis = 0)
self.gaussian_cov[c] = np.cov(proj, rowvar=False)
'''
Utility function to return the probability density for a gaussian, given an
input point, gaussian mean and covariance.
'''
def pdf(self, point, mean, cov):
cons = 1./((2*np.pi)**(len(point)/2.)*np.linalg.det(cov)**(-0.5))
return cons*np.exp(-np.dot(np.dot((point-mean),np.linalg.inv(cov)),(point-mean).T)/2.)
'''
Function to calculate error rates based on gaussian modeling.
'''
def calculate_score_gaussian(self, data):
classes = sorted(list(self.means.keys()))
inputs = self.drop_col(data, self.labelcol)
# project the inputs
proj = np.dot(self.w, inputs.T).T
# calculate the likelihoods for each class based on the gaussian models
likelihoods = np.array([[self.priors[c] * self.pdf([x[ind] for ind in
range(len(x))], self.gaussian_means[c],
self.gaussian_cov[c]) for c in
classes] for x in proj])
# assign prediction labels based on the highest probability
labels = np.argmax(likelihoods, axis = 1)
errors = np.sum(labels != data.ix[:, self.labelcol])
return errors
def plot_bivariate_gaussians(self):
classes = list(self.means.keys())
colors = cm.rainbow(np.linspace(0, 1, len(classes)))
plotlabels = {classes[c] : colors[c] for c in range(len(classes))}
fig = plt.figure()
ax3D = fig.add_subplot(111, projection='3d')
for c in self.means.keys():
data = np.random.multivariate_normal(self.gaussian_means[c],
self.gaussian_cov[c], size=100)
pdf = np.zeros(data.shape[0])
cons = 1./((2*np.pi)**(data.shape[1]/2.)*np.linalg.det(self.gaussian_cov[c])**(-0.5))
X, Y = np.meshgrid(data.T[0], data.T[1])
def pdf(point):
return cons*np.exp(-np.dot(np.dot((point-self.gaussian_means[c]),np.linalg.inv(self.gaussian_cov[c])),(point-self.gaussian_means[c]).T)/2.)
zs = np.array([pdf(np.array(ponit)) for ponit in zip(np.ravel(X),
np.ravel(Y))])
Z = zs.reshape(X.shape)
surf = ax3D.plot_surface(X, Y, Z, rstride=1, cstride=1,
color=plotlabels[c], linewidth=0,
antialiased=False)
plt.show()
def plot_proj_1D(self, data):
classes = list(self.means.keys())
colors = cm.rainbow(np.linspace(0, 1, len(classes)))
plotlabels = {classes[c] : colors[c] for c in range(len(classes))}
fig = plt.figure()
for i, row in data.iterrows():
proj = np.dot(self.w, row[:self.labelcol])
plt.scatter(proj, np.random.normal(0,1,1)+0, color =
plotlabels[row[self.labelcol]])
plt.show()
def plot_proj_2D(self, data):
classes = list(self.means.keys())
colors = cm.rainbow(np.linspace(0, 1, len(classes)))
plotlabels = {classes[c] : colors[c] for c in range(len(classes))}
fig = plt.figure()
for i, row in data.iterrows():
proj = np.dot(self.w, row[:self.labelcol])
plt.scatter(proj[0], proj[1], color =
plotlabels[row[self.labelcol]])
plt.show()
if __name__ == '__main__':
data = pd.read_csv(sys.argv[1])
labelcol = int(sys.argv[2])
lda = LDA(data, num_dims=2, convert_data=0, threshold=0, labelcol=labelcol)
trainerror, testerror = lda.fit()
print(trainerror)
print(testerror)
#print(verifyLDA(data, data, labelcol))
lda.plot_proj_2D(data)
lda.plot_bivariate_gaussians()
- fishers_lda.rar(300,5 KB)
Valora esta pregunta


0