Ayuda! en Matlab
Publicado por Josue (2 intervenciones) el 09/10/2015 02:40:45
Saludos
bueno soy nuevo en Matlab y quería saber si me pueden ayudar con los siguientes problemas:
Escriba un programa en Matlab que simule la siguiente situacion. Considere un colectivo de N monedas puestas encima de una mesa. Suponga que, al inicio, todas las monedas muestran "sol", Despues, use el generador de numeros randomisados de Matlab para seleccionar, en cada paso, una de las monedas; esta moneda se vuelve de "sol" a "aguila" o de "aguila" a "sol", las demas monedas no se cambian.
1.- Haga gráficas que muestran e desarrollo del numero de monedas con "aguila" Naguilas durante 10N pasos, para N=100 y N=1000 (e.g. para N=100 graficamos los primeros 1000 pasos).
2.- Para sistemas de carácter discreto, la entropia S de una configuración se calcula por la formula 1.
donde KB denotada la constante de boltzmann, g es el numero de posibles estados del sistema, y pn es la probabilidad de encontrar el sistema en el estado n. En nuestro caso, g es el numero de posibles estados de una sola moneda, es decir g=2, y hay solo dos probabiblidades., psol y paguila, donde psol es la probabilidad de encontrar "sol" en seleccionando una moneda de manera aleatoria; obiamente sera (la formula 2)
formula 2 psol=(Nsol)/(N)
Demuestre, que S con la definicion arriba es no-negativo, y que asuma su valor maximo cuando psol=paguila=1/2. Sigue, que este estado termodinamicamente corresponde al equilibrio termico, y que las graficas del inciso 1, muestran la tendencia de un sistema aleatorio de correr hacia el equilibrio termico empezando con un estado, que es muy lejos del mismo. Para cada una de las graficas del inciso 1. haga una grafica demostrando la evolucion de la entropia. La tendencia de la entropia de crecer hasta que alcanzo el equilibrio termico es la segunda ley de la termodinamica. Sin embargo, es muy importante darse cuenta, que para un cualquier N finito esta ley no aplica de manera exacta, hay pasos donde la entropia dismunuye, en ves de crecer; solo en el limite N--> infinito (el "limite termodinamico") se vuelve una ley exacta.
3.- Segun el Teorema de regresion de Poincare, para un cualquier N finito, y un cualquier estado inicial, el sistema regresara con incertidumbre, es decir, con probabilidad 1, a su estado inicial, si uno espera un tiempo suficiente. Deje correr su programa para algunos N pequeños. e.g N=10,20,30, hasta a que ocurre esto, es decir, que las monedas muestran todas "sol" otra ves. deberia observar, que el numero de pasos necesarios para observar este fenomeno crece rapidamente con N.
4.- Ahora, fije N=100, y deje correr su programa un gran de veces (por lo menos 100 veces). Haga una grafica de la distribucion de los valores Nsol obtenidos despues de estos 100 pasos (es decir, el eje horizontal tiene Nsol). Deberia obtener una grafica gaussiana. Esto provee una ilustracion de la ley del limite central.
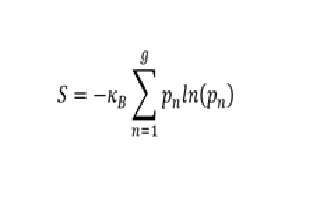
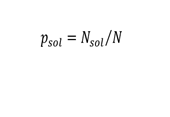
bueno soy nuevo en Matlab y quería saber si me pueden ayudar con los siguientes problemas:
Escriba un programa en Matlab que simule la siguiente situacion. Considere un colectivo de N monedas puestas encima de una mesa. Suponga que, al inicio, todas las monedas muestran "sol", Despues, use el generador de numeros randomisados de Matlab para seleccionar, en cada paso, una de las monedas; esta moneda se vuelve de "sol" a "aguila" o de "aguila" a "sol", las demas monedas no se cambian.
1.- Haga gráficas que muestran e desarrollo del numero de monedas con "aguila" Naguilas durante 10N pasos, para N=100 y N=1000 (e.g. para N=100 graficamos los primeros 1000 pasos).
2.- Para sistemas de carácter discreto, la entropia S de una configuración se calcula por la formula 1.
donde KB denotada la constante de boltzmann, g es el numero de posibles estados del sistema, y pn es la probabilidad de encontrar el sistema en el estado n. En nuestro caso, g es el numero de posibles estados de una sola moneda, es decir g=2, y hay solo dos probabiblidades., psol y paguila, donde psol es la probabilidad de encontrar "sol" en seleccionando una moneda de manera aleatoria; obiamente sera (la formula 2)
formula 2 psol=(Nsol)/(N)
Demuestre, que S con la definicion arriba es no-negativo, y que asuma su valor maximo cuando psol=paguila=1/2. Sigue, que este estado termodinamicamente corresponde al equilibrio termico, y que las graficas del inciso 1, muestran la tendencia de un sistema aleatorio de correr hacia el equilibrio termico empezando con un estado, que es muy lejos del mismo. Para cada una de las graficas del inciso 1. haga una grafica demostrando la evolucion de la entropia. La tendencia de la entropia de crecer hasta que alcanzo el equilibrio termico es la segunda ley de la termodinamica. Sin embargo, es muy importante darse cuenta, que para un cualquier N finito esta ley no aplica de manera exacta, hay pasos donde la entropia dismunuye, en ves de crecer; solo en el limite N--> infinito (el "limite termodinamico") se vuelve una ley exacta.
3.- Segun el Teorema de regresion de Poincare, para un cualquier N finito, y un cualquier estado inicial, el sistema regresara con incertidumbre, es decir, con probabilidad 1, a su estado inicial, si uno espera un tiempo suficiente. Deje correr su programa para algunos N pequeños. e.g N=10,20,30, hasta a que ocurre esto, es decir, que las monedas muestran todas "sol" otra ves. deberia observar, que el numero de pasos necesarios para observar este fenomeno crece rapidamente con N.
4.- Ahora, fije N=100, y deje correr su programa un gran de veces (por lo menos 100 veces). Haga una grafica de la distribucion de los valores Nsol obtenidos despues de estos 100 pasos (es decir, el eje horizontal tiene Nsol). Deberia obtener una grafica gaussiana. Esto provee una ilustracion de la ley del limite central.
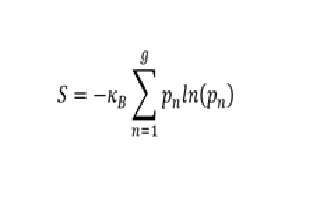
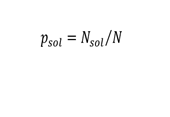
Valora esta pregunta


0

