Buscar un código de Python

Función que lea números ingresados por el usuario hasta que el usuario introduzca el 0. Después de esto, la función debe imprimir una tupla que contiene la cantidad de datos leídos, el producto de dichos números y el valor de la suma de los números pares y impares.

Si al realizar la ejecución "leerNumeros" el usuario introduce los siguientes valores:
3
2
-2
4
5
8
0
Se debería imprimir la tupla (6, -1920, 12, 8)

ya que el usuario digitó 6 números, el producto de dichos números es -1920 (-1920 = 3 · 2 · -2 · 4 · 5 · 8), la suma de los números pares es 12 (12 = 2 + (-2) + 4 + 8) y la suma de los números impares es 8 (8 = 3 + 5).

Funciones para obtener la los valores pares y impares de una lista, y funciones para obtener la cantidad de valores pares y impares de una lista.

Crear una función que puede recibir un numero o una cadena, y tiene que devolver una lista con los valores pares y impares.

Crear una función que recibe un numero entero y devuelve una lista con la cantidad de valores pares e impares contenidos en le numero recibido.

Dado un numero entero, crear una función que devuelva una lista con los números impares.

Crear una función que sume todos los valores pares de una comprendido entre dos números

Este simple código, solicita dos números enteros al usuario para sumar los números pares comprendidos entre los dos valores introducidos por el usuario.

**********************************************




Ejercicio: Aula_28_Transacion_Bit_Coin_Marzo_25.py
**************************************************
Formato RAW de la transacción BITCOIN
//////////////////////////////////////////////////////////////////

Propongo un ejercicio interesante. Datos de una transacción de Bitcoin en formato raw (hexadecimal).Cuando una transacción se crea, se representa en un formato hexadecimal binario. Pero luego, ¿Cómo se calcula el txid de una transacción en Bitcoin?. Pues, queridos alumnos, de eso va este ejercicio propuesto.
IDEA INICIAL DEL CÓDIGO.
Necesitamos hacer en Python, bajo Ubuntu, un programa ejemplo de una transacción en formato raw (hexadecimal), teniendo en cuenta que se deben aportar los datos ficticios, es decir para tener una salida en formato raw, de la transación y posteriormente lograr el cálculo que nos dará el txid, correspondiente. Este es el punto de partida, para que una vez optenidos todos los TXID, de todas las transacciones podramos obtener :
Una vez que tenemos todos los TXID de las transacciones de un bloque, los organizamos en un árbol de Merkle, - que ya vimos en un ejercicio anterior, que se construye aplicando doble SHA-256 a pares de hashes hasta obtener un único hash raíz (Merkle root).

¿Qué significa esto en la práctica?
El hash final del bloque (Block Hash) es el identificador único de ese bloque en la blockchain.
Este hash será el "hash del bloque anterior" en el siguiente bloque de la cadena, asegurando la integridad y seguridad de la blockchain.

Bien, los datos ficticios que aportaremos en nuestro programa serán los siguientes:
*******************************************************************************
Este formato hexadecimal incluye:
• Version de la transacción.
• Entradas (Inputs):
• Hash de la transacción previa (UTXO).
• Índice de salida (vout).
• Script de firma.
• Salidas (Outputs):
• Cantidad de satoshis enviados.
• Script de bloqueo (scriptPubKey).
• Locktime (para definir si se puede gastar en el futuro).

SIGNIFICADOS:
***********************
1. Versión de la transacción
Este es un número que indica la versión del formato de la transacción. A medida que el protocolo de Bitcoin evoluciona, pueden introducirse nuevas versiones para mejorar la funcionalidad y seguridad de las transacciones.

Actualmente, las versiones más comunes son 1 y 2.
La versión 2 se introdujo para admitir Replace-By-Fee (RBF), permitiendo reemplazar una transacción no confirmada con una versión de mayor comisión.
2. Entradas (Inputs)
Las entradas indican de dónde provienen los bitcoins que se están gastando en la transacción.

2.1. Hash de la transacción previa (UTXO)
Cada entrada hace referencia a una salida no gastada (UTXO, Unspent Transaction Output) de una transacción anterior. Para identificar de dónde provienen los fondos, se usa el hash de la transacción previa que contenía la salida que ahora queremos gastar.

Este hash es un identificador único de 256 bits (64 caracteres en hexadecimal).
Se obtiene aplicando SHA-256 dos veces a los datos de la transacción anterior.
2.2. Índice de salida (vout)
Dado que una transacción puede tener múltiples salidas, necesitamos especificar cuál de esas salidas estamos gastando.

vout es un número entero que indica el índice de la salida en la transacción anterior (comienza desde 0).
Ejemplo:
Si la transacción anterior tiene dos salidas y queremos gastar la segunda, vout será 1.

2.3. Script de firma
También llamado scriptSig, es un script que prueba que el usuario tiene permiso para gastar los bitcoins de la UTXO referenciada.

Contiene la firma digital generada con la clave privada del propietario de los bitcoins.
También incluye la clave pública del firmante.
Se ejecuta junto con el script de bloqueo (scriptPubKey) de la transacción anterior para validar la autenticidad del gasto.
3. Salidas (Outputs)
Cada salida define a dónde van los bitcoins en esta transacción.

3.1. Cantidad de satoshis enviados
Especifica la cantidad de bitcoins que se enviarán en esta salida, expresados en satoshis (1 BTC = 100,000,000 satoshis).

Ejemplo:
Si queremos enviar 0.01 BTC, la cantidad en satoshis será 1,000,000.

3.2. Script de bloqueo (scriptPubKey)
Es un script que define las condiciones para gastar esta salida en el futuro.

Generalmente, es un Pay-to-PubKey-Hash (P2PKH), que especifica que solo la persona que tenga la clave privada correspondiente a la clave pública hash puede gastar esos bitcoins.
También puede ser un Pay-to-Script-Hash (P2SH), Pay-to-Witness-PubKey-Hash (P2WPKH) u otros formatos de pago.
Ejemplo de scriptPubKey para una dirección P2PKH:


OP_DUP OP_HASH160 <PublicKeyHash> OP_EQUALVERIFY OP_CHECKSIG
4. Locktime (para definir si se puede gastar en el futuro)
Locktime es un campo opcional que define a partir de cuándo la transacción puede ser confirmada.

Si locktime es 0, la transacción se procesa inmediatamente.
Si es un número mayor que 500,000,000, representa una fecha en formato timestamp UNIX (segundos desde 1970).
Si es menor, representa el número de bloque a partir del cual la transacción será válida.
Ejemplo:

locktime = 800000 → Solo se confirmará después del bloque 800,000.
locktime = 1700000000 → Solo se confirmará después del 14 de noviembre de 2023 (según la fecha UNIX).
Resumen final
La transacción en Bitcoin tiene una versión para definir su formato.
Cada entrada (input) hace referencia a una UTXO anterior mediante su hash y un índice de salida (vout).
Para validar el gasto, la transacción incluye un script de firma (scriptSig).
Cada salida (output) especifica cuántos satoshis se envían y a quién, mediante un script de bloqueo (scriptPubKey).
Locktime puede definir un tiempo de espera antes de que la transacción sea válida.

**********************************************************************************

• Locktime (para definir si se puede gastar en el futuro).
Deberas de tener en cuenta que los datos aportados en formato hash, deberan ser chequeados para que cumplan las normas, es decir deben de ser exadecimales de 0 a 9, y letras de A a la F, sin espacios etc, si no eres cuidado en esto, el programa siempre dara errores.
Una vez que tengas la transacción en formato raw (hexadecimal), deberás Calcular el txid
1. Hash SHA-256 sobre los datos en formato hexadecimal.
2. Aplicar SHA-256 de nuevo al resultado del primer hash (doble SHA-256).
3. Invertir el orden de los bytes (little-endian).
Deberá verse por consola la transacion en formato Hexadecimal.
También deberá verse por consola el TXID.
Según la foto adjunta del programa.

*****************************************************************
No os explico aquí el programa, porque he intentado explicaros en el propio código
cada paso.
------------------------------------------------------------------------------------
Programa realizado en linux Ubuntu.
Con el editor sublime text.
Ejecución bajo consola linux:
python3 Aula_28_Transacion_Bit_Coin_Marzo_25.py
------------------------------------------------------------------------------------------

En las clases sucesivas, explicaremos dudas, que supongo serán muchas.

----------------------------------------------------------------------------------


python3 Aula_28_Arbol_Merkle_Marz_25.py
---------------------------------------


Problema, para el Aula 28, a estudiar por partes en la primera semana de Marzo/25.
***********************************************************************************************
Vamos a plantear hoy un clásico problema, muy habitual en la criptomoneda Bitcoin, donde se aplica el arbol de Merkle, para optener el hash final de las transaciones pertenecientes a un bloke, este dato es uno de los fundamentales con el fin de poder proceder a su minado.
Plantearemos el problema resumido de la siguiente forma:
Queremos desarrollar un arbol de Merkle, en python, en sistema operativo Ubuntu. Necesitamos que las entradas del árbol sean de 8 opciones por consola.Las entradas deben admitir datos alfanumericos. Deberemos optener el hash final del resultado del arbol, de los datos introducidos. El lenguaje que vamos a aplicar es python3, bajo un istema operativo linux ubuntu, trabajando en consola.
**************************************************
Inicialmente vamos a definir, para entenderlo, que es un árbol de Merkle.
------------------------------------------------------------------------
Bien. Decimos que un árbol de Merkle es una estructura de datos en forma de árbol binario que se usa para verificar la integridad y autenticidad de los datos de manera eficiente.
Se utiliza en criptografía, sistemas de archivos distribuidos, y , como hemos indicado antes, en los blockchain para asegurar que la información no ha sido alterada.
El aula, deberá profundizar un poco más en esta definición, con el fin de comprender su significado.

***************************************************************************************************
Este programa fue desarrollado con Python V3.
Editado con Sublime Text.
Bajo una plataforma Linux,
Ubuntu 20.04.6 LTS.
Ejecución bajo este comado en consola:
python3 Aula_28_Arbol_Merkle_Marz_25.py
**********************************************

EXPLICACION DE LOS PASOS DEL EJERCICIO PHYTHON.
------------------------------------------------------------------------------

1️⃣ Importación de Módulos de módulos
--------------------------------------
necesario para el desarrollo de python.

import hashlib
import networkx as nx
import matplotlib.pyplot as plt

hashlib: Se usa para calcular los hashes SHA-256 de los datos.
networkx: Permite crear y visualizar grafos (en este caso, el árbol de Merkle).
matplotlib.pyplot: Se usa para graficar el árbol de Merkle.

2️⃣ Función para Calcular el Hash de un Dato
---------------------------------------------

def hash_data(data):
return hashlib.sha256(data.encode()).hexdigest()
Recibe un data (cadena de texto).
Usa SHA-256 para calcular su hash hexadecimal y lo devuelve.

3️⃣ Construcción del Árbol de Merkle
------------------------------------

def merkle_tree_hash(data_list):
if len(data_list) % 2 != 0:
data_list.append(data_list[-1]) # Duplicar el último si es impar
Si la cantidad de datos es impar, se duplica el último dato para asegurar que haya pares.

hashes = [hash_data(data) for data in data_list]
tree_levels = [hashes]
Se generan los hashes SHA-256 de cada dato y se almacenan en la primera capa del árbol.

while len(hashes) > 1:
temp_hashes = []
for i in range(0, len(hashes), 2):
combined_hash = hash_data(hashes[i] + hashes[i + 1])
temp_hashes.append(combined_hash)
hashes = temp_hashes
tree_levels.append(hashes)

Se combinan de dos en dos, se concatenan y se vuelven a hashear hasta llegar a un único hash raíz.
Ejemplo de construcción:


Entradas: A, B, C, D, E, F, G, H
Nivel 0: hash(A), hash(B), hash(C), hash(D), hash(E), hash(F), hash(G), hash(H)
Nivel 1: hash(hash(A)+hash(B)), hash(hash(C)+hash(D)), hash(hash(E)+hash(F)), hash(hash(G)+hash(H))
Nivel 2: hash(hash_AB + hash_CD), hash(hash_EF + hash_GH)
Nivel 3 (Raíz): hash(hash_ABCD + hash_EFGH)

4️⃣ Dibujar el Árbol de Merkle
--------------------------------

def plot_merkle_tree(tree_levels):
G = nx.DiGraph()
pos = {}
level_offset = 2.5
node_id = 0
Se crea un grafo dirigido G para representar el árbol.
pos almacena las posiciones de los nodos.
level_offset controla la separación vertical de los niveles.

for level, nodes in enumerate(tree_levels):
y_pos = -level * level_offset
x_step = 2 ** (len(tree_levels) - level - 1)
for i, node in enumerate(nodes):
label = node if level == len(tree_levels) - 1 else node[:6] + "..."
pos[node_id] = (i * x_step, y_pos)
G.add_node(node_id, label=label)
node_id += 1
Se añaden nodos con etiquetas:
Se muestran solo los primeros 6 caracteres seguidos de ..., excepto en el hash final.

node_id = 0
for level in range(len(tree_levels) - 1):
for i in range(0, len(tree_levels[level]), 2):
parent_id = node_id + len(tree_levels[level])
G.add_edge(node_id, parent_id)
G.add_edge(node_id + 1, parent_id)
node_id += 2
Se añaden las conexiones entre nodos padre e hijos.

labels = nx.get_node_attributes(G, 'label')
plt.figure(figsize=(15, 10))
nx.draw(G, pos, with_labels=True, labels=labels, node_size=5000, node_color='lightblue', font_size=8, font_weight='bold', edge_color='gray')
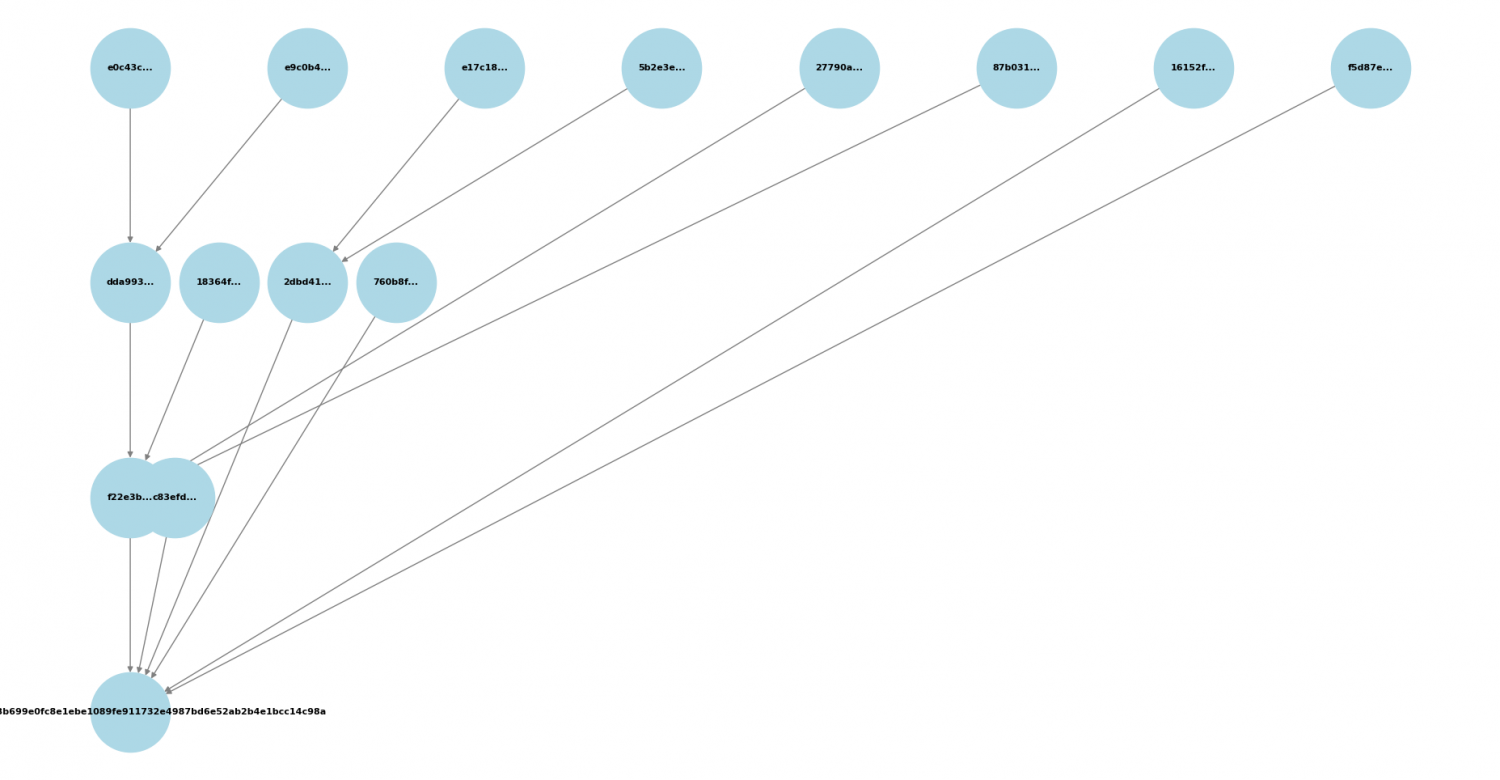
plt.title("Árbol de Merkle", fontsize=14)
plt.show()
Se genera la gráfica con matplotlib, usando networkx para dibujar el árbol.

5️⃣ Función Principal
----------------------

def main():
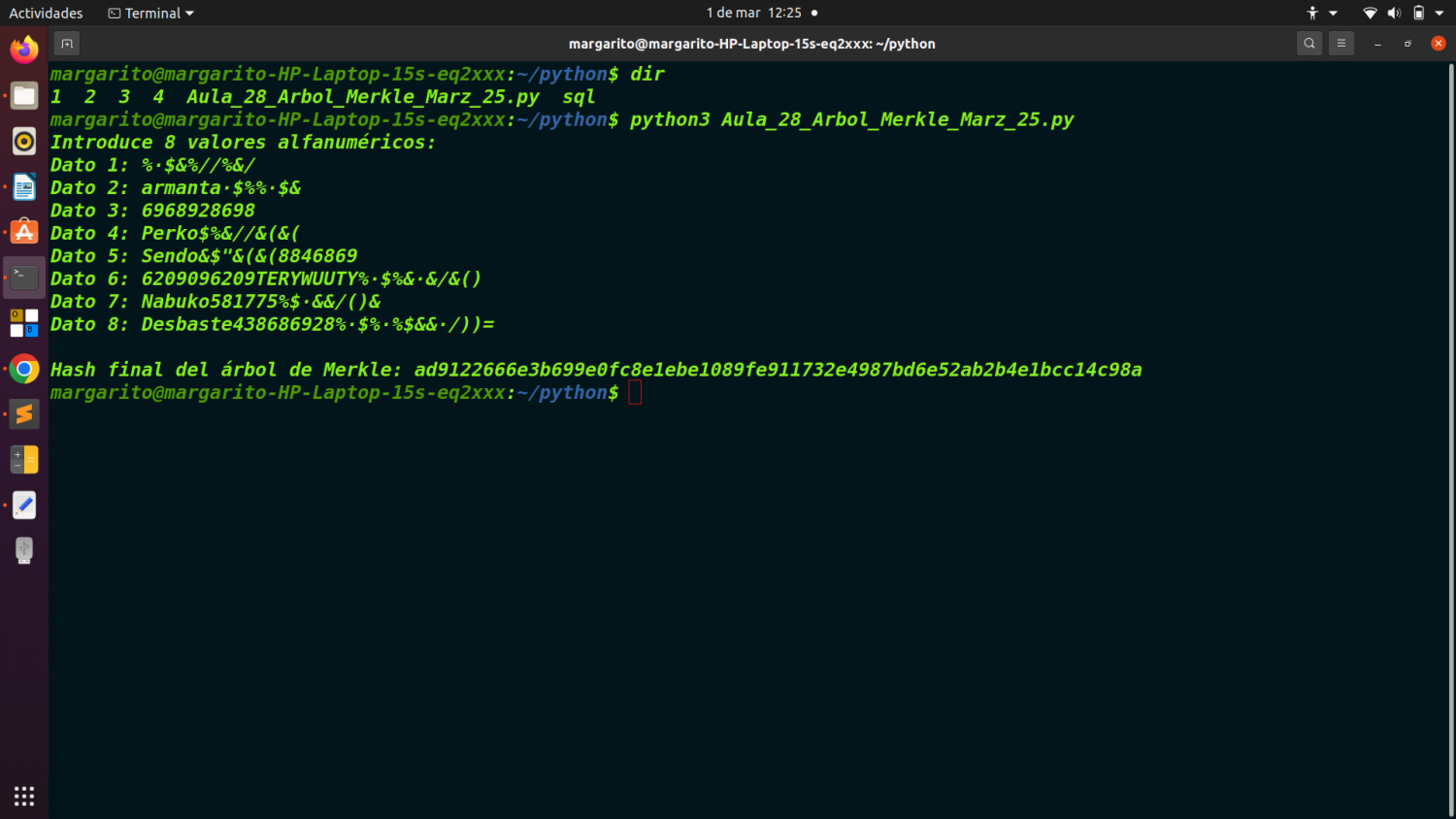
print("Introduce 8 valores alfanuméricos:")
data_list = [input(f"Dato {i+1}: ") for i in range(8)]
Se piden 8 entradas de datos por consola.

tree_levels = merkle_tree_hash(data_list)
root_hash = tree_levels[-1][0]
print("\nHash final del árbol de Merkle:", root_hash)
Se construye el árbol de Merkle.
Se imprime el hash raíz (Merkle Root).

plot_merkle_tree(tree_levels)
Se dibuja la gráfica del árbol.

6️⃣ Ejecución del Programa
----------------------------

if __name__ == "__main__":
main()
Se ejecuta main() solo si el script se ejecuta directamente.

********************************************************************
Ad augusta per angusta
**********************************************************************

Hilario Iglesias Martínez
/////////////////////////
Programa a ejecutar con GOOGLE COLAB.
************************************
Google Colab es un sistema de inteligencia artificial creado por Google. Se trata de un sistema que permite, aparte de otras cosas, el funcionamiento como IDE de forma que puedes interactuar en un entorno de programación Python, y su ejecución y prueba en linea.

Para poder utilizarlo, deberás darte de alta, con una referencia de correo en gmail.
Es indudable su potencia en los entornos de Inteligencia artificial. Tiene grandes prestaciones gráficas al utilizar los módulos TensorFlow -de google-y la biblioteca escrita en Python -en código abierto- llamada Keras, capaz de ejecutarse sobre TensorFlow.
**********************************************************************************
La red de ejmplo que planteamos aquí, es un sistema neuronal en modo Sequential, que indica que es un tipo de modelo de redes neuronales artificiales en el cual las capas se apilan de manera secuencial, una encima de la otra. Es el enfoque más básico y comúnmente utilizado en el aprendizaje profundo (deep learning) con la biblioteca de Python llamada Keras.

La creación de un modelo Sequential en Keras sigue los siguientes pasos generales:
con la siguiente linea de código.
from tensorflow.keras.models import Sequential


En Keras, el modo Sequential permite construir modelos de redes neuronales de forma secuencial, donde cada capa se agrega secuencialmente una tras otra. Cada capa se conecta a la siguiente en el flujo de información, pasando la salida de una capa como entrada a la siguiente.



***************************************************************************************************

El programa que pongo a continuación está realizado en en Python3, en un entorno Linux, Ubuntu 20.04.6 LTS. Se supone que por defecto ya tienes instalada esta versión de python.
----------------------------------------------------------------------------------
Deberás tener cargado el ejecutor de carga pip. La forma de instalarlo es la siguiente:
sudo apt update
sudo apt install python3-pip
----------------------------------------------------------------------------------
Una vez que lo tengas instalado ya podrás instalar también los modulos necesarios para Google Colab, de la siguiente forma:

pip install tensorflow
pip install keras

Dado que en el encabezado del programa nos encontramos estos módulos:

import numpy as np
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense

También deberemos comprobar que están cargados.
*************************************************************************
BASICAMENTE ESTA ES LA EXPLICACIÓN DEL PROGRAMA.
****************************************************
Este programa utiliza TensorFlow y Keras para crear y entrenar un modelo de red neuronal que predice la conversión de temperatura de Celsius a Fahrenheit. Aquí tienes una explicación paso a paso del programa:

Importa las bibliotecas necesarias:

numpy para manejar matrices y operaciones numéricas.
matplotlib.pyplot para visualizar los resultados.
Sequential de keras.models para crear un modelo de red neuronal secuencial.
Dense de keras.layers para agregar capas densamente conectadas a la red.
Crea los datos de entrada:

Define dos arrays de NumPy: Celsius y Fahrenheit, que contienen los pares de valores de temperatura para el entrenamiento del modelo.
Crea la red neuronal:

Inicializa un modelo secuencial llamado model.
Agrega tres capas densamente conectadas a la red:
La primera capa tiene 20 neuronas, utiliza la función de activación ReLU y espera un solo valor de entrada (input_dim=1).
La segunda capa tiene 10 neuronas y también utiliza la función de activación ReLU.
La tercera capa tiene una sola neurona y utiliza la función de activación lineal.
Compila el modelo:

Utiliza el optimizador Adam y la función de pérdida de error cuadrático medio (mean_squared_error).
Entrena el modelo:

Utiliza el método fit para entrenar el modelo con los datos de entrada Celsius y Fahrenheit.
Se especifican 20,000 rondas o vueltas de de entrenamiento -- con este dato se puede jugar empezando por valores más pequeños y viendo como va aumentando el aprendizaje-- y se establece verbose=0 para no mostrar la salida de entrenamiento durante el proceso.
Evalúa el modelo:

Utiliza el método evaluate para calcular la pérdida del modelo en los datos de entrada Celsius y Fahrenheit.
Imprime la pérdida del modelo.

Visualiza los resultados:

Grafica los datos de entrenamiento (Celsius y Fahrenheit) como puntos ('o').
Grafica las predicciones del modelo utilizando model.predict(Celsius) y una línea ('-').
Agrega etiquetas de los ejes y una leyenda para identificar los datos de entrenamiento y las predicciones del modelo.
Realiza una predicción:

Utiliza el modelo entrenado para predecir la temperatura en Fahrenheit para un valor de Celsius de 80.
Imprime la predicción resultante.
En resumen, este programa entrena un modelo de red neuronal para predecir la conversión de temperatura de Celsius a Fahrenheit y muestra los resultados a través de una visualización gráfica.

****************************************************************************
Si quieres puedes experimentar con el programa.
Busca en google -google Colab-
Informate del mismo, estudialo un poco, quizás lo encuentres apasionante.
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
EXPLICACIÓN PORMENORIZADA DE LAS LINEAS DE CÓDIGO
***********************************************************************************************************

"""
Importamos los módulos necesarios.
---------------------------------
import numpy as np ** Este Modulo permite trabajar con Arrays
import matplotlib.pyplot as plt **Este módulo permite trabajar con graficos
from keras.models import Sequential **Nos permite trabajar con redes secuenciales.
from keras.layers import Dense **"Dense" es un término utilizado para
referirse a una capa densamente conectada
o completamente conectada en una red neuronal.
"""

import numpy as np
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense

"""
Creamos la entrada de datos por medio de los arrays.
Les llamamos a las entradas Celsius y ahrenheit.
"""

Celsius = np.array([0, 10, 20, 30, 40, 50, 60, 70, 80, 90])
Fahrenheit = np.array([32, 50, 68, 86, 104, 122, 140, 158, 176, 194])

"""
Creamos la red neural.
---------------------
El modelo será de tipo secuencial, llamando a esa función.
en el módulo keras.models.

Dense(20): Esto indica que queremos agregar una capa densa con 20 neuronas.
Cada neurona en esta capa estará conectada a todas las
neuronas de la capa anterior y de la capa siguiente.

input_dim=1: Este argumento especifica la dimensión de la entrada a la capa.
En este caso, se indica que la capa recibirá una entrada unidimensional.
Esto significa que se espera una entrada de un solo valor.

activation='relu': Aquí se especifica la función de activación
que se utilizará en cada neurona de la capa. En este caso, se utiliza
la función de activación "ReLU" (Rectified Linear Unit).
La función ReLU es una función no lineal que se utiliza
comúnmente en redes neuronales y es conocida
por su capacidad para introducir no linearidad en el modelo.
*****************************************************************
ReLU(x) = max(0, x)
La función de activación ReLU (Rectified Linear Unit)
es una función no lineal ampliamente utilizada en
redes neuronales. La función ReLU se define de la siguiente manera:
para cualquier valor de entrada x, la función ReLU
devuelve 0 si x es negativo y x mismo si x es no negativo.

La función ReLU es popular en el campo del aprendizaje
profundo debido a sus propiedades deseables.
Algunas de las razones por las que se utiliza la función ReLU son:

No linealidad: La función ReLU introduce no linealidad
en la red neuronal, lo que permite que el modelo aprenda
relaciones no lineales entre las características de entrada.
Esto es esencial para capturar patrones complejos en los datos.

Eficiencia computacional: La función ReLU es computacionalmente
eficiente de calcular en comparación con funciones más complejas,
como la función sigmoide o la tangente hiperbólica.
Esto puede ser beneficioso, especialmente en redes neuronales profundas con muchas capas.

Evita el desvanecimiento del gradiente: En el entrenamiento de redes neuronales,
el desvanecimiento del gradiente puede ser un problema cuando las
derivadas de las funciones de activación son muy pequeñas.
La función ReLU evita este problema ya que tiene una derivada constante de 1 para x > 0, lo
que permite que los gradientes fluyan sin decaer rápidamente.

Sin embargo, una limitación de la función ReLU es que
no es diferenciable en x = 0.
Esto puede hacer que el entrenamiento sea más difícil
en algunos casos, especialmente cuando se utilizan
técnicas de optimización basadas en gradientes.
Para abordar este problema, se pueden utilizar variantes
suaves de la función ReLU, como la función Leaky ReLU o la función ReLU paramétrica,
que permiten cierto flujo de gradiente incluso para valores negativos de x.
****************************************************************
model.add(Dense(1, activation='linear'))

En una red neuronal, la función de activación 'linear'
(lineal) significa que no se aplica ninguna función de activación no lineal a
la salida de una capa específica.

Cuando se utiliza una función de activación lineal,
la salida de una neurona o capa simplemente se
calcula como una combinación lineal de las
entradas sin ninguna transformación no lineal
aplicada. Esto significa que la salida es
proporcionalmente igual a la suma ponderada de las entradas.

"""

model = Sequential()
model.add(Dense(20, input_dim=1, activation='relu'))
model.add(Dense(10, activation='relu'))
model.add(Dense(1, activation='linear'))


# Compilación del modelo
"""
En la compilación de un modelo de red neuronal, se especifican tres aspectos clave:

Función de pérdida (loss function): La función de pérdida define cómo se calcula
la discrepancia entre las salidas predichas por el modelo y las salidas reales o
etiquetas del conjunto de datos. El objetivo del entrenamiento es minimizar
esta función de pérdida. La elección de la función de pérdida depende del
tipo de problema que se esté abordando, como regresión,
clasificación binaria o clasificación multiclase.

Optimizador: El optimizador determina cómo se ajustan
los pesos y los sesgos de la red neuronal durante el
entrenamiento para minimizar la función de pérdida.
El optimizador utiliza algoritmos como el descenso de
gradiente estocástico (SGD) o algoritmos más avanzados
como Adam o RMSprop. Cada optimizador tiene sus propias
configuraciones y parámetros adicionales que se pueden
ajustar según sea necesario.

Métricas:
Las métricas se utilizan para evaluar el
rendimiento del modelo durante el entrenamiento
y la evaluación. Estas métricas proporcionan
información adicional sobre la precisión,
el error o cualquier otra medida relevante.
Algunas métricas comunes incluyen la precisión (accuracy)
para problemas de clasificación y el error cuadrático
medio (mean squared error) para problemas de regresión.

Después de configurar estos aspectos,
el modelo está listo para ser entrenado utilizando
los datos de entrenamiento proporcionados. Durante el
entrenamiento, el modelo utilizará la función de
pérdida y el optimizador para ajustar los pesos y
los sesgos de las capas de la red neuronal con el
objetivo de minimizar la pérdida y mejorar el
rendimiento en función de las métricas establecidas.


"""
model.compile(optimizer='adam', loss='mean_squared_error')

#Entrenamiento del modelo
"""[
El "entrenamiento del modelo" en una red neuronal se refiere
al proceso de ajustar los pesos y los sesgos de la red neuronal
utilizando un conjunto de datos de entrenamiento con el objetivo
de aprender patrones y relaciones en
los datos. Durante el entrenamiento, el modelo se expone
repetidamente a los ejemplos de entrenamiento,
calcula las salidas correspondientes y actualiza los parámetros
internos en función de la diferencia entre las salidas predichas y las salidas reales.

El entrenamiento de un modelo de red neuronal implica los siguientes pasos generales:

Inicialización de pesos: Los pesos y los sesgos de la red neuronal
se inicializan de forma aleatoria o mediante algún enfoque
específico, como la inicialización de Xavier o He.

Paso hacia adelante (Forward pass): Los datos de entrenamiento se propagan
a través de la red neuronal en una dirección, desde la capa de entrada
hasta la capa de salida. Las salidas se calculan mediante una
combinación lineal de los pesos y los sesgos, seguidos de
la aplicación de funciones de activación no lineales en cada capa.

Cálculo de la función de pérdida: Se compara la salida predicha
por el modelo con la salida real correspondiente del conjunto de
datos de entrenamiento utilizando una función de pérdida.
La función de pérdida mide qué tan bien se está desempeñando
el modelo en la tarea específica y proporciona una medida de
la discrepancia entre las salidas predichas y las salidas reales.

Retropropagación (Backpropagation):
El algoritmo de retropropagación se utiliza para calcular
las contribuciones relativas de cada peso y sesgo en la
función de pérdida. Se propaga el gradiente del error
hacia atrás a través de la red neuronal,
calculando las derivadas parciales de la función de
pérdida con respecto a cada peso y sesgo.
Estas derivadas se utilizan para actualizar
los pesos y sesgos mediante un proceso llamado optimización.

Optimización de los parámetros: Los pesos
y sesgos se actualizan utilizando un algoritmo
de optimización, como el descenso de gradiente
estocástico (SGD), Adam o RMSprop.
Estos algoritmos ajustan los parámetros de la
red neuronal en la dirección que reduce
la función de pérdida, utilizando la información
del gradiente calculada durante la retropropagación.

Repetición: Los pasos 2-5 se repiten para varios
ejemplos de entrenamiento hasta que se alcance un
criterio de detención, como un número máximo de iteraciones
(épocas) o una mejora aceptable en el rendimiento del modelo.

El proceso de entrenamiento busca encontrar
los valores óptimos para los pesos y sesgos de la
red neuronal que minimicen la función de pérdida, y
permitan que el modelo haga predicciones precisas en
datos no vistos. Una vez que el modelo está entrenado,
se puede utilizar para hacer predicciones en nuevos
ejemplos o para realizar otras tareas relacionadas con la inferencia.


"""
model.fit(Celsius, Fahrenheit, epochs=20000, verbose=0)

# Evaluación de el modelo
loss = model.evaluate(Celsius, Fahrenheit)
print('Loss:', loss)

# TRAZAR RESULTADOS.
"""
"Trazar los resultados" en una red neuronal se refiere a visualizar
o representar gráficamente los resultados obtenidos durante el entrenamiento o
la evaluación del modelo. La visualización de los resultados puede proporcionar
información importante sobre el rendimiento y el comportamiento del modelo,
así como ayudar a identificar posibles problemas o mejoras.

Aquí hay algunos tipos comunes de trazado de resultados en una red neuronal:

Gráficas de pérdida (Loss plots): Se representan gráficamente las curvas
de pérdida a lo largo de las épocas durante el entrenamiento. Esto muestra
cómo disminuye la pérdida a medida que el modelo se entrena y proporciona
información sobre la convergencia y la estabilidad del modelo.

Gráficas de métricas de rendimiento: Si se han definido métricas
de rendimiento adicionales, como la precisión o el error, se
pueden trazar para evaluar el rendimiento del modelo durante
el entrenamiento o la evaluación. Esto ayuda a comprender
cómo el rendimiento del modelo evoluciona a medida que se realiza el entrenamiento.

Visualización de predicciones: Se pueden trazar las predicciones
del modelo junto con las etiquetas reales para un conjunto de
datos de evaluación o pruebas. Esto permite comparar
visualmente las predicciones del modelo con los valores
reales y evaluar qué tan cerca están.

Mapas de calor (Heatmaps): En el caso de problemas de clasificación,
especialmente en clasificación de imágenes, se pueden utilizar mapas
de calor para visualizar las regiones de la imagen que el modelo
considera más importantes para tomar una decisión de clasificación.
Estos mapas de calor resaltan las áreas de la imagen que
tienen un mayor impacto en las predicciones del modelo.

Representaciones de características (Feature representations):
En redes neuronales convolucionales, se pueden trazar las
representaciones aprendidas en diferentes capas de la red
para visualizar cómo las características se transforman a
medida que se profundiza en la red. Esto puede ayudar a
entender qué tipo de características o patrones la red
está aprendiendo a reconocer.

La visualización de los resultados en una red
neuronal puede proporcionar una comprensión más
profunda del rendimiento del modelo y ayudar en el
análisis y la mejora del mismo. Además, los gráficos y
visualizaciones pueden ser útiles para comunicar los
resultados a otras personas de manera más intuitiva.

"""

plt.plot(Celsius, Fahrenheit, 'o')
plt.plot(Celsius, model.predict(Celsius), '-')
plt.xlabel('Celsius')
plt.ylabel('Fahrenheit')
plt.legend(['Training data', 'Linear regression'], loc='best')
plt.show()
celsius_value = 100
fahrenheit_prediction = model.predict(np.array([80]))
print('Prediccion para Hilario:', fahrenheit_prediction[0])
#Fórmula habitual de cálculo por un algoritmo con esta formula
#(80 °C × 9 / 5) + 32 = 176 °F