Iniciar sesiónCerrar
Correo:
Contraseña:
Entrar
Recordar sesión en este navegador
Iniciar sesiónIniciar sesiónCrear cuentaCrear cuenta
LWP » Código Fuente » n

Mostrar los tags: n

Volver
Agregar Código Fuente
Mostrando del 511 al 520 de 2.742 coincidencias
<<>>
Se ha buscado por el tag: n
Imágen de perfil

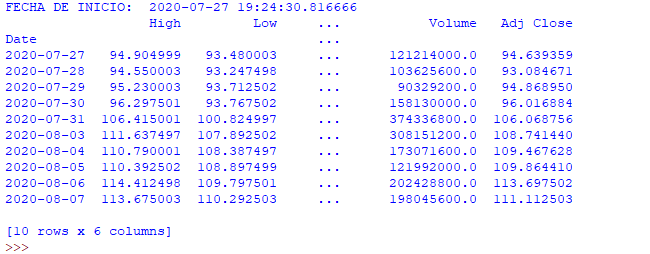
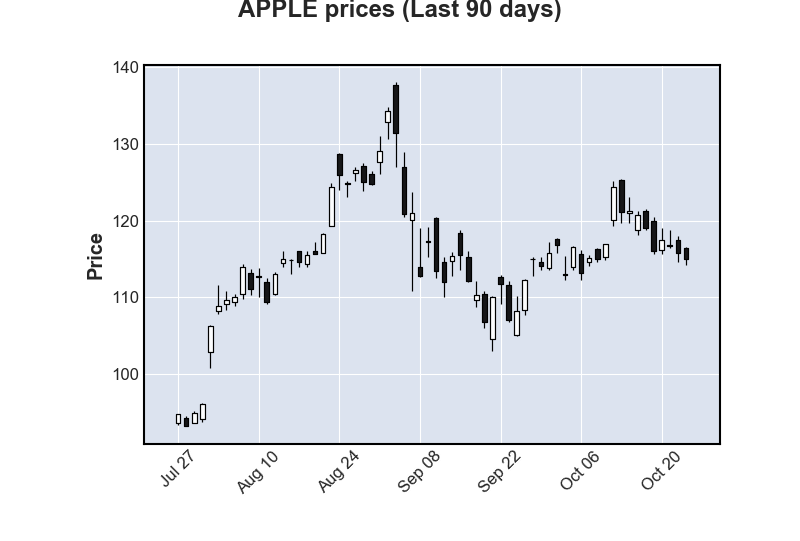
GRÁFICO DE VELAS (PARA ANÁLISIS FINANCIERO).


Python

Publicado el 25 de Octubre del 2020 por Antonio (77 códigos)
5.643 visualizaciones desde el 25 de Octubre del 2020
El siguiente script muestra el gráfico de velas, en el que se expresan los valores de cotización máximo, mínimo, de apertura y cierre, correspondientes a la la compañía "Apple" durante los últimos 90 días. Los datos se obtienen directamente de la página de "Yahoo finance".
appa

Figure_1
Imágen de perfil

Sumar los dígitos de un numero en PHP


PHP

Publicado el 23 de Octubre del 2020 por Kata (76 códigos)
5.800 visualizaciones desde el 23 de Octubre del 2020
Crear una función que reciba un entero y devuelva la suma de sus valores.

1
2
3
4
5
sumarNumeros(11111); // 5
sumarNumeros(1230); // 6
sumarNumeros(1231); // 7
sumarNumeros(00); // 0
sumarNumeros(1); // 1
Imágen de perfil

Validar el formato de un numero telefónico en Python


Python

Publicado el 21 de Octubre del 2020 por Katas (150 códigos)
9.160 visualizaciones desde el 21 de Octubre del 2020
Función para validar un numero de teléfono de 11 dígitos numéricos separados en grupos de tres por el guion (-), algo así: 12-123-123-123

1
2
3
4
5
6
7
validarTelefono("12-123-123-123") # True
validarTelefono("12-123-123-12") # False
validarTelefono("2-123-123-123") # False
validarTelefono("12-13-123-123") # False
validarTelefono("12-123-1a3-123") # False
validarTelefono("12/123-123-123") # False
validarTelefono("12-123123-123") # False
Imágen de perfil

Numero Top en Python


Python

Publicado el 20 de Octubre del 2020 por Katas (150 códigos)
2.690 visualizaciones desde el 20 de Octubre del 2020
Crear una función que al recibir un numero entero, verifique que si al sumar las cifras del número y dividirlo por su cantidad de cifras. el resultado es un numero primo. Si es así, se dice que es un numero top.

Ejemplo: 177 seria: 1+7+7=15/3=5
el 5 si es un numero primo

Ejemplo: 1771 seria: 1+7+7+1=16/4=4
el 4 no es un numero primo

1
2
numeroTop(177) # 1+7+7=15/3=5 = True
numeroTop(1771) # 1+7+7+1=16/4=4 = False


NOTA: Si la función no recibe un entero, devuelve una excepción.
1...Anterior4748495051525354555657Siguiente...275