Problema al usar FMINCON
Publicado por Carlos (2 intervenciones) el 13/11/2018 09:18:00
Buenos días, aprovecho para presentarme, mi nombre es Carlos y soy estudiante de ingeniería. Mi acceso a este foro siempre ha sido de consulta, hasta ahora, ya que tengo un problema que no consigo solucionar y me gustaría encontrar a alguien que me echara una mano.
Voy a tratar de explicarlo de la forma más breve y precisa (adjuntando los archivos necesarios) para que sea lo más claro y rápido para todos.
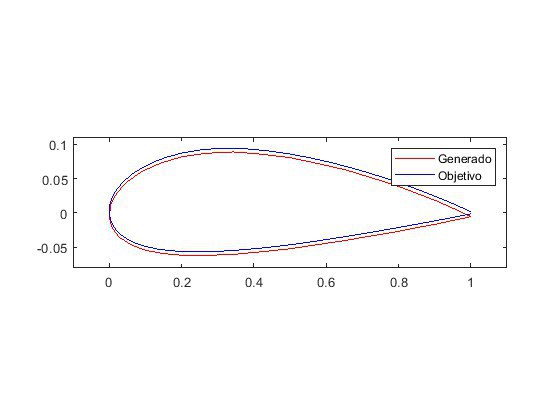
Tengo una forma geométrica dada en coordenadas 'x' e 'y'. Después tengo una función que calcula una serie de propiedades 'cp' de esta geometría. El caso, es que calcula 'cp' en unas nuevas variables 'xc' e 'yc' que no son más que los puntos medios entre las coordenadas 'x' e 'y' (esto se denomina método de paneles por si alguno le suena).
Y ahora el problema: dados unos valores 'xc' y 'cp' objetivos quiero, con la ayuda de la función FMINCON, que a partir de unos datos 'x' e 'y' iniciales se encuentren los valores 'x' e 'y' que consiguen generar el target 'xc' y 'cp' mencionado.
Os adjunto el código a continuación en forma de texto, y en forma de archivo (adjunto también la función que calcula cp por si queréis ejecutarlo)
Muchas gracias de antemano y un saludo a ver si consigo encontrar una solución, o al menos aclarar las dudas! Quedo a vuestra disposición para resolver vuestras cuestiones y explicaros lo que necesitéis.
PD: Si quitáis la línea de 'yc_opt' podréis ejecutar el código sin errores y ver un poco mejor de lo que hablo.
Voy a tratar de explicarlo de la forma más breve y precisa (adjuntando los archivos necesarios) para que sea lo más claro y rápido para todos.
Tengo una forma geométrica dada en coordenadas 'x' e 'y'. Después tengo una función que calcula una serie de propiedades 'cp' de esta geometría. El caso, es que calcula 'cp' en unas nuevas variables 'xc' e 'yc' que no son más que los puntos medios entre las coordenadas 'x' e 'y' (esto se denomina método de paneles por si alguno le suena).
Y ahora el problema: dados unos valores 'xc' y 'cp' objetivos quiero, con la ayuda de la función FMINCON, que a partir de unos datos 'x' e 'y' iniciales se encuentren los valores 'x' e 'y' que consiguen generar el target 'xc' y 'cp' mencionado.
Os adjunto el código a continuación en forma de texto, y en forma de archivo (adjunto también la función que calcula cp por si queréis ejecutarlo)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
clear all; close all; clc;
% Valores iniciales
x = [1.0000000e+00 9.9384417e-01 9.7552826e-01 9.4550326e-01 9.0450850e-01 8.5355339e-01 7.9389263e-01 7.2699525e-01 6.5450850e-01 5.7821723e-01 5.0000000e-01 4.2178277e-01 3.4549150e-01 2.7300475e-01 2.0610737e-01 1.4644661e-01 9.5491503e-02 5.4496738e-02 2.4471742e-02 6.1558297e-03 0.0000000e+00 6.1558297e-03 2.4471742e-02 5.4496738e-02 9.5491503e-02 1.4644661e-01 2.0610737e-01 2.7300475e-01 3.4549150e-01 4.2178277e-01 5.0000000e-01 5.7821723e-01 6.5450850e-01 7.2699525e-01 7.9389263e-01 8.5355339e-01 9.0450850e-01 9.4550326e-01 9.7552826e-01 9.9384417e-01 1.0000000e+00];
y = [0.0000000e+00 -9.2117646e-04 -3.6090289e-03 -7.8530303e-03 -1.3349811e-02 -1.9752282e-02 -2.6706343e-02 -3.3864077e-02 -4.0874975e-02 -4.7367248e-02 -5.2935330e-02 -5.7146848e-02 -5.9574461e-02 -5.9848087e-02 -5.7714126e-02 -5.3083229e-02 -4.6048933e-02 -3.6866546e-02 -2.5893313e-02 -1.3503368e-02 0.0000000e+00 1.3503368e-02 2.5893313e-02 3.6866546e-02 4.6048933e-02 5.3083229e-02 5.7714126e-02 5.9848087e-02 5.9574461e-02 5.7146848e-02 5.2935330e-02 4.7367248e-02 4.0874975e-02 3.3864077e-02 2.6706343e-02 1.9752282e-02 1.3349811e-02 7.8530303e-03 3.6090289e-03 9.2117646e-04 0.0000000e+00];
theta = 0;% Valores objetivos
xc_target = [9.9688476e-01 9.8450868e-01 9.6008973e-01 9.2427659e-01 8.7800690e-01 8.2247449e-01 7.5909260e-01 6.8945450e-01 6.1529136e-01 5.3842725e-01 4.6082908e-01 3.8464321e-01 3.1159182e-01 2.4306956e-01 1.8060008e-01 1.2560858e-01 7.9393234e-02 4.3101798e-02 1.7696386e-02 3.9112883e-03 2.2445414e-03 1.2931185e-02 3.5866682e-02 7.0595006e-02 1.1632953e-01 1.7195390e-01 2.3604257e-01 3.0690443e-01 3.8263106e-01 4.6095369e-01 5.3978998e-01 6.1743437e-01 6.9204925e-01 7.6179528e-01 8.2497153e-01 8.8005498e-01 9.2573517e-01 9.6094179e-01 9.8486375e-01 9.9695941e-01];
cp_target = [5.5471634e-01 2.9922504e-01 2.1080566e-01 1.4781156e-01 9.8517613e-02 5.7192248e-02 1.9854700e-02 -1.6621324e-02 -5.4487941e-02 -9.4713590e-02 -1.3565899e-01 -1.7489953e-01 -2.1916582e-01 -2.7113632e-01 -3.2118723e-01 -3.5855358e-01 -3.6277750e-01 -2.8018730e-01 5.0379485e-02 7.7073395e-01 8.9347165e-01 1.9260211e-01 -2.8344384e-01 -5.0606686e-01 -6.1166160e-01 -6.5379568e-01 -6.5362232e-01 -6.2134328e-01 -5.6032980e-01 -4.8542694e-01 -4.1263804e-01 -3.4260057e-01 -2.7320726e-01 -2.0281263e-01 -1.2929243e-01 -5.0141472e-02 3.7529936e-02 1.3791065e-01 2.6073036e-01 5.4526003e-01];
% Valor inicial de la variable que se debe modificar para alcanzar el cp_target
yc_inicial = [-4.6058823e-04 -2.2651027e-03 -5.7310296e-03 -1.0601421e-02 -1.6551047e-02 -2.3229313e-02 -3.0285210e-02 -3.7369526e-02 -4.4121112e-02 -5.0151289e-02 -5.5041089e-02 -5.8360654e-02 -5.9711274e-02 -5.8781107e-02 -5.5398678e-02 -4.9566081e-02 -4.1457740e-02 -3.1379930e-02 -1.9698341e-02 -6.7516841e-03 6.7516841e-03 1.9698341e-02 3.1379930e-02 4.1457740e-02 4.9566081e-02 5.5398678e-02 5.8781107e-02 5.9711274e-02 5.8360654e-02 5.5041089e-02 5.0151289e-02 4.4121112e-02 3.7369526e-02 3.0285210e-02 2.3229313e-02 1.6551047e-02 1.0601421e-02 5.7310296e-03 2.2651027e-03 4.6058823e-04];
% Función que devuelve valores objetivos a partir de valores iniciales
[xc, yc, cp] = vortex_panel_method(x, y, theta);
% Optimización
diferencia = sum((cp-cp_target).^2);
yc_opt = fmincon(diferencia, yc_inicial);
% Muestra resultados
disp(['Diferencia inicial: ' num2str(diferencia)])
plot(xc_target, cp_target, 'ro')
hold on
plot(xc, cp, 'bx')
hold on
plot(x, y)
hold on
plot(xc,yc_opt)
legend('Objetivo','Inicial','Perfil 0','Perfil 1')
ylabel('CP')
xlabel('XC')
Muchas gracias de antemano y un saludo a ver si consigo encontrar una solución, o al menos aclarar las dudas! Quedo a vuestra disposición para resolver vuestras cuestiones y explicaros lo que necesitéis.
PD: Si quitáis la línea de 'yc_opt' podréis ejecutar el código sin errores y ver un poco mejor de lo que hablo.
- codigo.zip(2,9 KB)
Valora esta pregunta


0