"""
Derivada_Descenso_Gradiente_2.py
Que hace el programa:
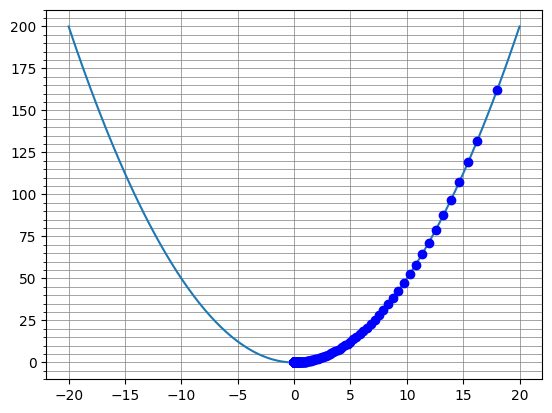
Dada la parábola de esta función:
f(x)=(x ** 2 / 2)
Vamos a realizar la derivada inversa a partir
de un punto dado por:
init_x = 18.
También imprimiremos su valor mínimo.
"""
import numpy as np
import matplotlib.pyplot as plt
def Mi_Funcion(x):
return (x**2/2)
def Hacer_Derivada(x):
return (x)
x=np.linspace(-20,20,250)
print("****************************************************************")print("Imprimimos los valores de la matriz desde x=-20 a x=20")print("****************************************************************")print(x)
print("****************************************************************")print('\n')y=Mi_Funcion(x)
print("****************************************************************")print("Imprimimos los valores de la matriz para el eje y.")print("****************************************************************")print(y)
print("****************************************************************")print('\n')#Inicializamos un punto cualquiera, por ejemplo iniciamos x en 18.
Inicio_x=18
#Establecemos el coeficiente de aprendizaje learnin rate, inicialmente en 0.05
lr=0.05
#Definimos el punto de partida aplicando derivada y coeficiente de aprendizaje.
Punto_x=Inicio_x-Hacer_Derivada(Inicio_x)*lr
Iniciar_y=Mi_Funcion(Inicio_x)
print("****************************************************************")print("Puntos iniciales en y, y en x respectivamente en y :",Iniciar_y,"y en x:",Inicio_x)print("****************************************************************")print('\n')#Comenzamos a diseñar la gráfica.
plt.plot(x,y)
#Señalamos el unto de inicio.
plt.plot(Inicio_x,Iniciar_y,'bo')
Punto_Minimo_Derivado=Hacer_Derivada(Punto_x)
print(Punto_Minimo_Derivado)
Minimo_Punto_x=Punto_x
print(Minimo_Punto_x)
#Utilizamos range para todos los puntos.
for i in range(1000):
Punto_x=Punto_x-Hacer_Derivada( Punto_x)*lr
Iniciar_y=Mi_Funcion(Punto_x)
plt.plot( Punto_x,Iniciar_y, 'bo')
#Vamos a imprimir el valor del ultímo número más aproximado a 0 utilizando un condicional.
Punto_Derivado_Actual=Hacer_Derivada( Punto_x)
if Punto_Derivado_Actual<Punto_Minimo_Derivado:
Punto_Derivado_Actual=Punto_Minimo_Derivado
Minimo_Punto_x=Punto_x
#Vamos a colocar en la grafica una cuadricula para una mejor vision y referencia de valores
plt.grid(True, which='both', linestyle='-', linewidth=0.5, color='gray') # Cambia el linestyle y el linewidth
plt.minorticks_on
#************************************************************
# Ajustar el espaciado de las minorticks en los ejes x e y (puedes ajustar estos valores según tus necesidades)
plt.xticks(minor=True) # Esto activará las minorticks en el eje x
plt.yticks(minor=True) # Esto activará las minorticks en el eje y
# Ajustar las minor ticks en los ejes x e y
plt.minorticks_on()
plt.gca().xaxis.set_minor_locator(plt.MultipleLocator(5)) # Cambia el valor para ajustar el espaciado en el eje x
plt.gca().yaxis.set_minor_locator(plt.MultipleLocator(5)) # Cambia el valor para ajustar el espaciado en el eje y
#***********************************************************
print("Valor mínimo del punto coincidente con la mínima derivada: {:.122f}".format(Punto_x))plt.show()
"""
****************************************************************
Imprimimos los valores de la matriz desde x=-20 a x=20
****************************************************************
[-20. -19.83935743 -19.67871486 -19.51807229 -19.35742972
-19.19678715 -19.03614458 -18.87550201 -18.71485944 -18.55421687
-18.3935743 -18.23293173 -18.07228916 -17.91164659 -17.75100402
-17.59036145 -17.42971888 -17.26907631 -17.10843373 -16.94779116
-16.78714859 -16.62650602 -16.46586345 -16.30522088 -16.14457831
-15.98393574 -15.82329317 -15.6626506 -15.50200803 -15.34136546
-15.18072289 -15.02008032 -14.85943775 -14.69879518 -14.53815261
-14.37751004 -14.21686747 -14.0562249 -13.89558233 -13.73493976
-13.57429719 -13.41365462 -13.25301205 -13.09236948 -12.93172691
-12.77108434 -12.61044177 -12.4497992 -12.28915663 -12.12851406
-11.96787149 -11.80722892 -11.64658635 -11.48594378 -11.3253012
-11.16465863 -11.00401606 -10.84337349 -10.68273092 -10.52208835
-10.36144578 -10.20080321 -10.04016064 -9.87951807 -9.7188755
-9.55823293 -9.39759036 -9.23694779 -9.07630522 -8.91566265
-8.75502008 -8.59437751 -8.43373494 -8.27309237 -8.1124498
-7.95180723 -7.79116466 -7.63052209 -7.46987952 -7.30923695
-7.14859438 -6.98795181 -6.82730924 -6.66666667 -6.5060241
-6.34538153 -6.18473896 -6.02409639 -5.86345382 -5.70281124
-5.54216867 -5.3815261 -5.22088353 -5.06024096 -4.89959839
-4.73895582 -4.57831325 -4.41767068 -4.25702811 -4.09638554
-3.93574297 -3.7751004 -3.61445783 -3.45381526 -3.29317269
-3.13253012 -2.97188755 -2.81124498 -2.65060241 -2.48995984
-2.32931727 -2.1686747 -2.00803213 -1.84738956 -1.68674699
-1.52610442 -1.36546185 -1.20481928 -1.04417671 -0.88353414
-0.72289157 -0.562249 -0.40160643 -0.24096386 -0.08032129
0.08032129 0.24096386 0.40160643 0.562249 0.72289157
0.88353414 1.04417671 1.20481928 1.36546185 1.52610442
1.68674699 1.84738956 2.00803213 2.1686747 2.32931727
2.48995984 2.65060241 2.81124498 2.97188755 3.13253012
3.29317269 3.45381526 3.61445783 3.7751004 3.93574297
4.09638554 4.25702811 4.41767068 4.57831325 4.73895582
4.89959839 5.06024096 5.22088353 5.3815261 5.54216867
5.70281124 5.86345382 6.02409639 6.18473896 6.34538153
6.5060241 6.66666667 6.82730924 6.98795181 7.14859438
7.30923695 7.46987952 7.63052209 7.79116466 7.95180723
8.1124498 8.27309237 8.43373494 8.59437751 8.75502008
8.91566265 9.07630522 9.23694779 9.39759036 9.55823293
9.7188755 9.87951807 10.04016064 10.20080321 10.36144578
10.52208835 10.68273092 10.84337349 11.00401606 11.16465863
11.3253012 11.48594378 11.64658635 11.80722892 11.96787149
12.12851406 12.28915663 12.4497992 12.61044177 12.77108434
12.93172691 13.09236948 13.25301205 13.41365462 13.57429719
13.73493976 13.89558233 14.0562249 14.21686747 14.37751004
14.53815261 14.69879518 14.85943775 15.02008032 15.18072289
15.34136546 15.50200803 15.6626506 15.82329317 15.98393574
16.14457831 16.30522088 16.46586345 16.62650602 16.78714859
16.94779116 17.10843373 17.26907631 17.42971888 17.59036145
17.75100402 17.91164659 18.07228916 18.23293173 18.3935743
18.55421687 18.71485944 18.87550201 19.03614458 19.19678715
19.35742972 19.51807229 19.67871486 19.83935743 20. ]
****************************************************************
****************************************************************
Imprimimos los valores de la matriz para el eje y.
****************************************************************
[2.00000000e+02 1.96800052e+02 1.93625909e+02 1.90477573e+02
1.87355043e+02 1.84258318e+02 1.81187400e+02 1.78142288e+02
1.75122982e+02 1.72129482e+02 1.69161788e+02 1.66219900e+02
1.63303818e+02 1.60413542e+02 1.57549072e+02 1.54710408e+02
1.51897550e+02 1.49110498e+02 1.46349252e+02 1.43613813e+02
1.40904179e+02 1.38220351e+02 1.35562330e+02 1.32930114e+02
1.30323704e+02 1.27743101e+02 1.25188303e+02 1.22659312e+02
1.20156127e+02 1.17678747e+02 1.15227174e+02 1.12801406e+02
1.10401445e+02 1.08027290e+02 1.05678941e+02 1.03356397e+02
1.01059660e+02 9.87887292e+01 9.65436041e+01 9.43242851e+01
9.21307721e+01 8.99630651e+01 8.78211642e+01 8.57050693e+01
8.36147804e+01 8.15502976e+01 7.95116208e+01 7.74987500e+01
7.55116853e+01 7.35504266e+01 7.16149740e+01 6.97053273e+01
6.78214868e+01 6.59634522e+01 6.41312237e+01 6.23248012e+01
6.05441848e+01 5.87893744e+01 5.70603700e+01 5.53571717e+01
5.36797794e+01 5.20281931e+01 5.04024129e+01 4.88024387e+01
4.72282705e+01 4.56799084e+01 4.41573523e+01 4.26606022e+01
4.11896582e+01 3.97445202e+01 3.83251883e+01 3.69316624e+01
3.55639425e+01 3.42220287e+01 3.29059209e+01 3.16156191e+01
3.03511234e+01 2.91124337e+01 2.78995500e+01 2.67124724e+01
2.55512008e+01 2.44157352e+01 2.33060757e+01 2.22222222e+01
2.11641748e+01 2.01319334e+01 1.91254980e+01 1.81448686e+01
1.71900453e+01 1.62610280e+01 1.53578168e+01 1.44804116e+01
1.36288124e+01 1.28030193e+01 1.20030322e+01 1.12288511e+01
1.04804761e+01 9.75790713e+00 9.06114418e+00 8.39018726e+00
7.74503637e+00 7.12569152e+00 6.53215271e+00 5.96441993e+00
5.42249319e+00 4.90637248e+00 4.41605781e+00 3.95154917e+00
3.51284657e+00 3.09995000e+00 2.71285947e+00 2.35157497e+00
2.01609651e+00 1.70642409e+00 1.42255770e+00 1.16449735e+00
9.32243028e-01 7.25794745e-01 5.45152498e-01 3.90316285e-01
2.61286108e-01 1.58061967e-01 8.06438606e-02 2.90317898e-02
3.22575442e-03 3.22575442e-03 2.90317898e-02 8.06438606e-02
1.58061967e-01 2.61286108e-01 3.90316285e-01 5.45152498e-01
7.25794745e-01 9.32243028e-01 1.16449735e+00 1.42255770e+00
1.70642409e+00 2.01609651e+00 2.35157497e+00 2.71285947e+00
3.09995000e+00 3.51284657e+00 3.95154917e+00 4.41605781e+00
4.90637248e+00 5.42249319e+00 5.96441993e+00 6.53215271e+00
7.12569152e+00 7.74503637e+00 8.39018726e+00 9.06114418e+00
9.75790713e+00 1.04804761e+01 1.12288511e+01 1.20030322e+01
1.28030193e+01 1.36288124e+01 1.44804116e+01 1.53578168e+01
1.62610280e+01 1.71900453e+01 1.81448686e+01 1.91254980e+01
2.01319334e+01 2.11641748e+01 2.22222222e+01 2.33060757e+01
2.44157352e+01 2.55512008e+01 2.67124724e+01 2.78995500e+01
2.91124337e+01 3.03511234e+01 3.16156191e+01 3.29059209e+01
3.42220287e+01 3.55639425e+01 3.69316624e+01 3.83251883e+01
3.97445202e+01 4.11896582e+01 4.26606022e+01 4.41573523e+01
4.56799084e+01 4.72282705e+01 4.88024387e+01 5.04024129e+01
5.20281931e+01 5.36797794e+01 5.53571717e+01 5.70603700e+01
5.87893744e+01 6.05441848e+01 6.23248012e+01 6.41312237e+01
6.59634522e+01 6.78214868e+01 6.97053273e+01 7.16149740e+01
7.35504266e+01 7.55116853e+01 7.74987500e+01 7.95116208e+01
8.15502976e+01 8.36147804e+01 8.57050693e+01 8.78211642e+01
8.99630651e+01 9.21307721e+01 9.43242851e+01 9.65436041e+01
9.87887292e+01 1.01059660e+02 1.03356397e+02 1.05678941e+02
1.08027290e+02 1.10401445e+02 1.12801406e+02 1.15227174e+02
1.17678747e+02 1.20156127e+02 1.22659312e+02 1.25188303e+02
1.27743101e+02 1.30323704e+02 1.32930114e+02 1.35562330e+02
1.38220351e+02 1.40904179e+02 1.43613813e+02 1.46349252e+02
1.49110498e+02 1.51897550e+02 1.54710408e+02 1.57549072e+02
1.60413542e+02 1.63303818e+02 1.66219900e+02 1.69161788e+02
1.72129482e+02 1.75122982e+02 1.78142288e+02 1.81187400e+02
1.84258318e+02 1.87355043e+02 1.90477573e+02 1.93625909e+02
1.96800052e+02 2.00000000e+02]
****************************************************************
****************************************************************
Puntos iniciales en y, y en x respectivamente en y : 162.0 y en x: 18
****************************************************************
Valor mínimo del punto coincidente con la mínima derivada: 0.00000000000000000000090490168986440381148303409332768965143107148274314261240675733022342797085002530366182327270507812500
"""