Código de Python - Recordatorio, descenso con momentum

***********************************************************************************************************************
Aula_28_repaso_descenso_momentum.py
+++++++++++++++++++++++++++++++++++
Dado que existen numerosas dudas sobre la aplicación de momentúm a un descenso de gradiente.
Vamos a explicar, lo más fácil posible, en que consiste, aunquue se miráis hacía atrás encontrareis
ejercicios en esta WEB, en la que se habla de este tema con ejercicios de ejemplo.

Sí suponéis una función ondulada, sobre dos ejes coordenados, en que el eje y tiene los valores de pérdida, y el eje x tiene los valores de parámetros o entradas. Esta función ondulada tendrá diversos, valores locales mínimos, y un valor, digamos, global mínimo.
Al aplicar un momentum, lo que hacemos es que en estos valles el descenso de gradiente no se relentice, hasta llegar global mínimo.

Bien, vamos a concretar en el siguiente resumen, las particulatidades del momentum.
Luego, plantearemos el sencillo ejercicio: Aula_28_repaso_descenso_momentum.py, para ver su funcionamiento real.

*****************************************************************************************************************

El descenso de gradiente con momentum (o SGD con momentum, por sus siglas en inglés) es una variación del algoritmo de descenso de gradiente estocástico (SGD) que se utiliza para entrenar redes neuronales y otros modelos de aprendizaje automático.

El objetivo del descenso de gradiente es encontrar los parámetros óptimos de un modelo que minimicen la función de error.
En el caso de las redes neuronales, la función de error representa la diferencia entre las predicciones del modelo y los datos reales.

El descenso de gradiente funciona iterativamente, ajustando los parámetros del modelo en la dirección del gradiente negativo de la función de error. Esto significa que los parámetros se mueven en la dirección hacía abajo que más reduce el error.
Sin embargo, el descenso de gradiente estándar puede ser sensible al ruido en los datos y puede quedar atrapado en mínimos locales, los valles de los que hablamos anteriormente.

Aquí es donde entra en juego el momentum. El momentum introduce una especie de "memoria" en el algoritmo, lo que le permite tener en cuenta los gradientes anteriores al actualizar los parámetros. Esto ayuda a suavizar las actualizaciones y a evitar
que el algoritmo se quede oscilando o se atasque en mínimos locales.

En términos matemáticos, el momentum se implementa mediante un término adicional en la ecuación de actualización de los parámetros.
Este término es proporcional al gradiente promedio de las iteraciones anteriores y ayuda a impulsar los parámetros en la misma dirección según los cálculos más favorables para un descenso que sea optimizado.

El uso del momentum tiene varias ventajas:

Aumenta la velocidad de convergencia: El momentum puede ayudar a que el algoritmo converja al mínimo global de la función de error más rápidamente.

Reduce las oscilaciones: El momentum ayuda a suavizar las actualizaciones de los parámetros, lo que puede reducir las oscilaciones en la trayectoria del aprendizaje.

Escapa de los mínimos locales: El momentum puede ayudar al algoritmo a escapar de los mínimos locales, que son puntos en los que la función de error es localmente mínima pero no globalmente mínima.

El momentum se controla mediante un hiperparámetro llamado coeficiente de momentum, que suele estar entre 0 y 1. Un valor más alto del coeficiente de momentum da más importancia a los gradientes anteriores y puede aumentar la velocidad de convergencia, pero también puede hacer que el algoritmo sea más sensible al ruido.

En general, el descenso de gradiente con momentum es una técnica poderosa para entrenar redes neuronales y otros modelos de aprendizaje automático.
Es más rápido y más robusto que el descenso de gradiente estándar, y puede ayudar a mejorar el rendimiento general del modelo.
********************************************************************************************************************
Como dijimos anteriormente proponemos ahora el ejercicio:
Aula_28_repaso_descenso_momentum.py, que pasamos a explicar:

1-Lo primero que hacemos es importar las librerías necesarias.

En nuestro caso: Se importan las librerías necesarias: numpy para cálculos numéricos y matplotlib.pyplot para graficar los resultados.

2-Definimos la Función de Pérdida y su Gradiente.

# Función de pérdida (En nuestro caso escogemos un ejemplo simple: f(x) = x^2)
def loss_function(x):
return x**2

# Gradiente o derivada de la función de pérdida
def gradient(x):
return 2*x

3- Ahora definimos los arámetros Iniciales.

x = np.random.randn() # Con el fin de no complicarnos la vida
utilizamos random en una inicialización aleatoria de los valores de x.
learning_rate = 0.1 Esto sería el ratio de aprendizaje.
momentum = 0.9 El coeficiente del momento
velocity = 0 Y lo inicializamos con un valor 0.

4- Almacenamiento de Pérdidas con el fin de poder realizar la gráfica.
losses = [ ]

5- Ahora lo que tenemos que hacer es el bucle de entrenamiento.

Iteraciones de entrenamiento con 200 iteraciones o ciclos.

for i in range(200):
grad = gradient(x)
velocity = momentum * velocity - learning_rate * grad
x += velocity
loss = loss_function(x)
losses.append(loss)
print(f"Iteración {i+1}, x: {x}, Loss: {loss}")

El bucle de entrenamiento se ejecuta durante 200 iteraciones. En cada iteración
Se calcula el gradiente de la función de pérdida en el punto actual
Se actualiza la velocidad usando la fórmula del momentum:
Se actualiza el valor de x, sumándole la velocidad: velocity x += velocity.
Se calcula la pérdida actual usando la función de pérdida.
Se almacena el valor de la pérdida en la lista losses.
Se imprime el número de iteración, el valor de x, conla pérdida correspondiente.


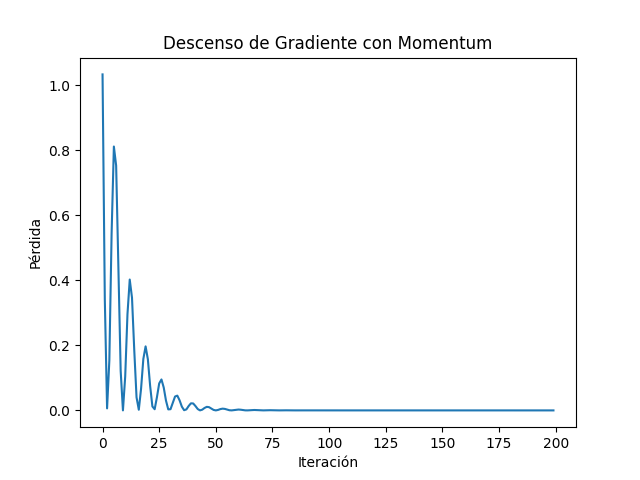
5-Con el fin de hacer más intuitivo el ejercicio graficamos las pérdidas.

plt.plot(losses)
plt.xlabel('Iteración')
plt.ylabel('Pérdida')
plt.title('Descenso de Gradiente con Momentum')
plt.show()

---------------------------------------------------------------------------
--------------------------------------------------------------------------
Para este ejercicio hemos utilizado una plataforma Linux, con Ubuntu 20.04.6 LTS.
Lo hemos editado con Sublite text.
La versión de python es la 3.
Se debe tener cargado para su importación en el sistema, estos módulos:
import numpy as np
import matplotlib.pyplot as plt
*****************************************************
Ejecución bajo consola linux:
python3 Aula_28_repaso_descenso_momentum.py

*****************************************************