Código de Python - Repaso graficos con matplotlib

**********************************************************************************************************************

Repaso-matplotlib-Aula-38-uranio-235.py
------------------------------------------------------
Con la idea de repasar la librería matplotlib, propongo este sencillo ejercicio de la representación aleatoria de un átomo de Uranio-235.
El ejercicio es de ejecución sencilla, y puede el alunno jugar con sus datos de entrada.
La librería matplotlib, es de uso habitual en todos los programas graficados, incluidos
los de inteligencia artificial.
----------------------------------------------------------------------------------------
Vamos a dar una pequeña descripción de Física cuántica, con el fin de entender este desarrollo.
********************************************************************************************
En la física cuántica, la idea de electrones orbitando alrededor del núcleo en trayectorias definidas, como planetas alrededor del sol, es incorrecta y ha sido reemplazada por un modelo más complejo y preciso.

En el modelo cuántico, los electrones no tienen órbitas definidas. En cambio, se describen mediante funciones de onda, que son soluciones a la ecuación de Schrödinger. Estas funciones de onda no nos dicen la trayectoria exacta de un electrón, sino la probabilidad de encontrar un electrón en una determinada región del espacio alrededor del núcleo. Esta región donde es más probable encontrar al electrón se llama "orbital".

Los orbitales tienen diferentes formas y tamaños, y cada uno corresponde a un nivel de energía específico. Los orbitales son esféricos, los p tienen forma de mancuerna, los d y f son más complejos. La densidad de probabilidad, que es la interpretación de la función de onda, nos da una "nube electrónica" donde la densidad de esta nube es mayor en las regiones donde es más probable encontrar al electrón.

En resumen:

Modelo Cuántico: En lugar de órbitas definidas, los electrones existen en "nubes de probabilidad" llamadas orbitales.
Funciones de Onda: Describen la probabilidad de encontrar un electrón en una determinada región del espacio.
Orbitales: Las diferentes formas (s, p, d, f) corresponden a diferentes distribuciones de probabilidad y niveles de energía.
Así que, efectivamente, los electrones están en un estado de movimiento continuo y no podemos determinar su posición exacta, sino solo la probabilidad de encontrarlo en un lugar determinado en un momento dado.


********************************************************************

Podemos crear una visualización simple utilizando la biblioteca matplotlib en Python para representar el núcleo atómico y una nube de electrones en movimiento aleatorio. A continuación, os presento el código Repaso-matplotlib-Aula-38-uranio-235.py
para crear esta simulación:

Este código hace lo siguiente:

Configuración inicial: Define el número de electrones y el límite del espacio donde se moverán.
Posiciones iniciales: Genera posiciones iniciales aleatorias para los electrones dentro de un cubo centrado en el núcleo.
Gráfico: Configura el gráfico 3D utilizando matplotlib.
Núcleo y electrones: Dibuja el núcleo en el centro y los electrones en sus posiciones iniciales.
Función de actualización: Mueve los electrones aleatoriamente en cada fotograma, asegurándose de que permanezcan dentro de los límites definidos.
Animación: Utiliza FuncAnimation de matplotlib para animar el movimiento de los electrones.
Este es un modelo simplificado y no representa fielmente la mecánica cuántica, pero da una buena visualización de un núcleo y una nube de electrones moviéndose aleatoriamente alrededor
de él.

*****************************************************************************************

Umbral de órbita extrema: Se define una variable umbral_extremo que establece el límite a partir del cual consideramos que un electrón está en la órbita extrema.
Función de actualización:
Se calcula la distancia de cada electrón al núcleo usando np.linalg.norm.
Se separan los electrones en dos grupos: normales y extremos, según la distancia calculada.
Se limpian y vuelven a dibujar todos los elementos del gráfico en cada fotograma.
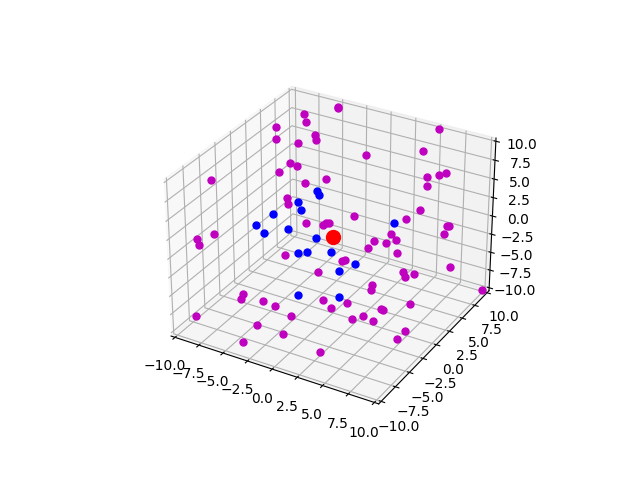
Se plotean los electrones normales en azul y los extremos en rosa.
Esto resaltará los electrones que están a punto de salirse de la órbita con un color rosa en la animación.

********************************************************************************************
Realizado en Linux, ubuntu.
Ejecución.
python3 Repaso-matplotlib-Aula-38-uranio-235.py