Mostrar los tags: es
Mostrando del 21 al 30 de 735 coincidencias
Se ha buscado por el tag: es
-----------------------------------------------------------------------------
La clasificación de datos mediante árboles de decisiones es un método de aprendizaje automático que se utiliza para categorizar o etiquetar datos en diferentes clases o categorías. Es una técnica de modelado predictivo que se basa en la creación de un "árbol" de decisiones, donde cada nodo interno del árbol representa una pregunta o una prueba sobre una característica específica de los datos, y las ramas que salen de ese nodo conducen a diferentes resultados o decisiones basadas en el valor de esa característica. Los nodos hoja del árbol representan las categorías o clases en las que se divide el conjunto de datos.
El proceso de clasificación a través de árboles de decisión implica:
Construcción del árbol: Se inicia con un nodo raíz que representa todo el conjunto de datos. Luego, se selecciona una característica y un umbral que se utilizará para dividir los datos en dos subconjuntos. Este proceso se repite recursivamente en cada subconjunto hasta que se alcanza un criterio de parada, como un tamaño máximo de profundidad del árbol, una cantidad mínima de muestras en los nodos hoja, o una impureza mínima.
Selección de características: En cada paso de división, se elige la característica que mejor separa los datos, lo que se logra al minimizar alguna métrica de impureza, como el índice de Gini o la entropía. La característica y el umbral que minimizan la impureza se utilizan para dividir los datos en dos ramas.
Predicción: Una vez construido el árbol, se utiliza para hacer predicciones sobre datos nuevos. Los datos nuevos se introducen en el árbol, siguiendo las ramas que corresponden a las características de esos datos, hasta llegar a un nodo hoja que representa la clase predicha.
Los árboles de decisión son atractivos porque son interpretables y fáciles de visualizar. Sin embargo, pueden ser propensos al sobreajuste (overfitting), especialmente si se construyen árboles muy profundos. Para abordar este problema, se pueden utilizar técnicas como la poda (pruning) o el uso de bosques aleatorios (random forests) que combinan múltiples árboles para mejorar la precisión y reducir el sobreajuste.
En resumen, la clasificación de datos mediante árboles de decisión es una técnica poderosa y ampliamente utilizada en aprendizaje automático para tareas de clasificación, donde el objetivo es predecir la categoría o clase a la que pertenecen los datos de entrada en función de sus características.Ejercicio sencillo para aprendizaje de un descenso de gradiente tipo estocástico.
----------------------------------------------------------------------------------------------------------
Descenso de Gradiente Estocástico (Stochastic Gradient Descent, SGD):
El descenso de gradiente estocástico es un enfoque de optimización en el que se actualizan los parámetros del modelo utilizando un solo ejemplo de entrenamiento o un pequeño subconjunto de ejemplos (mini-batch) en cada iteración.
En cada iteración, se selecciona aleatoriamente un ejemplo o un mini-batch para calcular el gradiente y actualizar los parámetros.
SGD es mucho más eficiente computacionalmente que el muestreo histórico de costos y es especialmente útil cuando se tienen grandes conjuntos de datos, ya que permite un entrenamiento más rápido y escalable.
En resumen, el muestreo histórico de costos utiliza todo el conjunto de datos en cada iteración, mientras que el descenso de gradiente estocástico utiliza un subconjunto aleatorio de datos en cada iteración. SGD tiende a ser más ruidoso debido a su aleatoriedad, pero puede converger a una solución aceptable en menos iteraciones. Ambos enfoques tienen sus ventajas y desventajas, y la elección entre ellos depende de las características del problema y los recursos computacionales disponibles. También existen variantes intermedias, como el Mini-batch Gradient Descent, que utilizan un tamaño de mini-batch moderado para combinar eficiencia y estabilidad en el entrenamiento de modelos.
"""
Hilario Iglesias Martínez.
*****************************************
Ejercicio:
CuadernoEstocas-Aula-48-15-SEP-RV-2.py
-----------------------------------------
Ejecución:python3 CuadernoEstocas-Aula-48-15-SEP-RV-2.py
******************************************
Se prueba con los valores con pareamétros mínimos,
con el fin de apreciar su funcionamiento:
learning_rate = 0.01
n_iterations = 4
np.random.seed(0)
X = 2 * np.random.rand(4, 1)
y = 4 + 3 * X + np.random.randn(4, 1)
-------------------------------------------
Creado bajo plataforma Linux.
Ubuntu 20.04.6 LTS
Editado con Sublime Text.
Ejecutado bajo consola linux:
python3 CuadernoEstocas-Aula-48-15-SEP-RV-2.py
"""Hilario Iglesias Marínez
*******************************************************************
Ejercicio:
Estocástico_Aula_F-890.py
Ejecucion bajo Consola Linux:
python3 Estocástico_Aula_F-890.py
******************************************************************
Diferencias.
El descenso de gradiente es un algoritmo de optimización utilizado comúnmente en el aprendizaje automático y la optimización de funciones. Hay dos variantes principales del descenso de gradiente: el descenso de gradiente tipo Batch (también conocido como descenso de gradiente por lotes) y el descenso de gradiente estocástico. Estas dos variantes difieren en la forma en que utilizan los datos de entrenamiento para actualizar los parámetros del modelo en cada iteración.
Descenso de Gradiente Tipo Batch:
En el descenso de gradiente tipo Batch, se utiliza el conjunto completo de datos de entrenamiento en cada iteración del algoritmo para calcular el gradiente de la función de costo con respecto a los parámetros del modelo.
El gradiente se calcula tomando el promedio de los gradientes de todas las muestras de entrenamiento.
Luego, se actualizan los parámetros del modelo utilizando este gradiente promedio.
El proceso se repite hasta que se alcanza una convergencia satisfactoria o se ejecuta un número predefinido de iteraciones.
Descenso de Gradiente Estocástico (SGD):
En el descenso de gradiente estocástico, en cada iteración se selecciona una sola muestra de entrenamiento al azar y se utiliza para calcular el gradiente de la función de costo.
Los parámetros del modelo se actualizan inmediatamente después de calcular el gradiente para esa única muestra.
Debido a la selección aleatoria de muestras, el proceso de actualización de parámetros es inherentemente más ruidoso y menos suave que en el descenso de gradiente tipo Batch.
SGD es más rápido en cada iteración individual y a menudo converge más rápidamente, pero puede ser más ruidoso y menos estable en términos de convergencia que el descenso de gradiente tipo Batch.
Diferencias clave:
Batch GD utiliza todo el conjunto de datos en cada iteración, lo que puede ser costoso computacionalmente, mientras que SGD utiliza una sola muestra a la vez, lo que suele ser más eficiente en términos de tiempo.
Batch GD tiene una convergencia más suave y estable debido a que utiliza gradientes promedio, mientras que SGD es más ruidoso pero a menudo converge más rápido.
Batch GD puede quedar atrapado en óptimos locales, mientras que SGD puede escapar de ellos debido a su naturaleza estocástica.
En la práctica, también existen variantes intermedias como el Mini-Batch Gradient Descent, que utiliza un pequeño conjunto de datos (mini-lote) en lugar del conjunto completo, equilibrando así los beneficios de ambas técnicas. La elección entre estas variantes depende de la naturaleza del problema y las restricciones computacionales.
[
b]AulaF_658-Gradiente_Estocastico.py
*************************************************[/b]
El descenso de gradiente estocástico (SGD por sus siglas en inglés, Stochastic Gradient Descent) es un algoritmo de optimización ampliamente utilizado en el campo del aprendizaje automático y la inteligencia artificial para entrenar modelos de machine learning, especialmente en el contexto de aprendizaje profundo (deep learning). SGD es una variante del algoritmo de descenso de gradiente clásico.
La principal diferencia entre el descenso de gradiente estocástico y el descenso de gradiente tradicional radica en cómo se actualizan los parámetros del modelo durante el proceso de entrenamiento. En el descenso de gradiente tradicional, se calcula el gradiente de la función de pérdida utilizando todo el conjunto de datos de entrenamiento en cada paso de la optimización, lo que puede ser computacionalmente costoso en conjuntos de datos grandes.
En contraste, en SGD, en cada paso de optimización se utiliza un único ejemplo de entrenamiento (o un pequeño lote de ejemplos de entrenamiento) de forma aleatoria. Esto introduce estocasticidad en el proceso, ya que el gradiente calculado en cada paso se basa en una muestra aleatoria de datos. Como resultado, el proceso de optimización es más rápido y puede converger a un mínimo local o global de la función de pérdida de manera más eficiente en muchos casos.
Los pasos generales del algoritmo de descenso de gradiente estocástico son los siguientes:
Inicializar los parámetros del modelo de manera aleatoria o utilizando algún valor inicial.
Mezclar aleatoriamente el conjunto de datos de entrenamiento.
Realizar iteraciones sobre el conjunto de datos de entrenamiento, tomando un ejemplo (o un pequeño lote) a la vez.
Calcular el gradiente de la función de pérdida con respecto a los parámetros utilizando el ejemplo seleccionado.
Actualizar los parámetros del modelo utilizando el gradiente calculado y una tasa de aprendizaje predefinida.
Repetir los pasos 3-5 durante un número fijo de iteraciones o hasta que se cumpla un criterio de convergencia.
El uso de SGD es beneficioso en situaciones donde el conjunto de datos es grande o cuando se necesita un entrenamiento rápido. Sin embargo, la estocasticidad puede hacer que el proceso sea más ruidoso y requiera una sintonización cuidadosa de hiperparámetros, como la tasa de aprendizaje. Además, existen variantes de SGD, como el Mini-Batch Gradient Descent, que toman un pequeño lote de ejemplos en lugar de uno solo, lo que ayuda a suavizar las actualizaciones de parámetros sin la necesidad de calcular el gradiente en todo el conjunto de datos.Hilario Iglesias Martínez.
******************************************************************************************
ClaseAula-F896.py
***************************************************************************************
Este ejercicio, sencillo, para aprendizaje y seguimiento de los parámetros: peso,sesgo,costo, en un descenso de gradiente tipo Batch.
***************************************************************************************
Los términos "peso", "sesgo" y "costo" pueden tener diferentes significados dependiendo del contexto en el que se utilicen. Aquí te proporcionaré una breve descripción de cada uno de estos términos en diversos contextos:
Peso (Weight):
En el contexto de la física, el peso se refiere a la fuerza gravitatoria que actúa sobre un objeto debido a la atracción de la gravedad de la Tierra. Se mide en unidades de fuerza, como newtons o libras.
En el aprendizaje automático y la inteligencia artificial, un "peso" se refiere a los coeficientes asociados con las conexiones entre neuronas en una red neuronal. Estos pesos determinan la fuerza y dirección de la influencia de una neurona en otra dentro de la red. Los pesos se ajustan durante el proceso de entrenamiento de la red para que la red pueda aprender y realizar tareas específicas.
Sesgo (Bias):
En el contexto de la estadística y el análisis de datos, el sesgo se refiere a la tendencia sistemática de un conjunto de datos o un modelo estadístico a producir resultados que se desvían de la verdad o de la población real debido a errores sistemáticos en el proceso de recopilación o modelado de datos.
En el aprendizaje automático, el sesgo (bias) es un término que se utiliza para referirse a un valor constante añadido a la salida de una función en una red neuronal. El sesgo permite que la red pueda modelar funciones más complejas, desplazando la función de activación. Es una especie de "ajuste" que ayuda a la red a aprender y generalizar mejor.
Costo (Cost):
En el ámbito empresarial y financiero, el costo se refiere a la cantidad de recursos (dinero, tiempo, esfuerzo, etc.) que se requiere para producir o realizar algo. Puede incluir costos directos e indirectos.
En matemáticas y optimización, el costo es una medida de la cantidad que se desea minimizar o maximizar en un problema. Por ejemplo, en la optimización lineal, se busca minimizar una función de costo sujeta a ciertas restricciones.
En el contexto del aprendizaje automático y la optimización de modelos, el costo es una medida de cuán bien está funcionando un modelo en relación con los datos de entrenamiento y se utiliza para ajustar los parámetros del modelo durante el proceso de entrenamiento. El objetivo es minimizar el costo para que el modelo se ajuste mejor a los datos y pueda realizar predicciones precisas en nuevos datos.
Estos son conceptos que pueden ser ampliamente aplicados en diversos campos y contextos, por lo que su significado puede variar según el contexto específico en el que se utilicen.*****************************************************************************************************
Hilario Iglesias Martínez
ClaseViernes-F543.py
DESCENSO DE GRADIENTE BATCH
*********************************************************************************************************
El "descenso de gradiente tipo Batch" es una técnica de optimización utilizada en el aprendizaje automático y la estadística para ajustar los parámetros de un modelo matemático, como una regresión lineal o una red neuronal, de manera que se minimice una función de costo específica. Es una de las variantes más simples y fundamentales del descenso de gradiente.
Aquí tienes una explicación de cómo funciona el descenso de gradiente tipo Batch:
Inicialización de parámetros: Comienza con un conjunto inicial de parámetros para tu modelo, que generalmente se eligen de manera aleatoria o se establecen en valores iniciales.
Selección de lote (Batch): En el descenso de gradiente tipo Batch, se divide el conjunto de datos de entrenamiento en lotes o subconjuntos más pequeños. Cada lote contiene un número fijo de ejemplos de entrenamiento. Por ejemplo, si tienes 1000 ejemplos de entrenamiento, puedes dividirlos en lotes de 32 ejemplos cada uno.
Cálculo del gradiente: Para cada lote, calculas el gradiente de la función de costo con respecto a los parámetros del modelo. El gradiente es una medida de cómo cambia la función de costo cuando se hacen pequeños ajustes en los parámetros. Indica la dirección en la que debes moverte para minimizar la función de costo.
Actualización de parámetros: Después de calcular el gradiente para cada lote, promedias los gradientes de todos los lotes y utilizas ese gradiente promedio para actualizar los parámetros del modelo. Esto se hace multiplicando el gradiente promedio por una tasa de aprendizaje (learning rate) y restando ese valor de los parámetros actuales. El learning rate controla el tamaño de los pasos que das en la dirección del gradiente.
Repetición: Los pasos 2-4 se repiten varias veces (llamadas épocas) a través de todo el conjunto de datos de entrenamiento. Cada época consiste en procesar todos los lotes y ajustar los parámetros del modelo.
Convergencia: El proceso de ajuste de parámetros continúa hasta que se alcanza un criterio de convergencia, que generalmente se establece en función de la precisión deseada o el número de épocas.
El descenso de gradiente tipo Batch es eficiente en términos de cómputo, ya que utiliza todos los datos de entrenamiento en cada paso de actualización de parámetros. Sin embargo, puede ser lento en conjuntos de datos grandes, y su convergencia puede ser más lenta en comparación con otras variantes del descenso de gradiente, como el descenso de gradiente estocástico (SGD) o el mini-batch SGD.
En resumen, el descenso de gradiente tipo Batch es una técnica de optimización que ajusta los parámetros de un modelo mediante el cálculo y la actualización de gradientes en lotes de datos de entrenamiento, con el objetivo de minimizar una función de costo. Es una parte fundamental en la optimización de modelos de aprendizaje automático.
*********************************************************************************************************
Ejecucion.
Bajo consola de Linux.
python3 ClaseViernes-F543.py"""
Derivada_Descenso_Gradiente.py
-----------------------------------
Que hace el programa:
Dada la parábola de esta función:
f(x,t)=(x ** 2 / 2) + t
Vamos a realizar la derivada de los puntos de una parábola
de forma inversa, lo que se define como descenso de gradiente,
a partir de un punto dado por:
init_x = 18.
Muy utilizado en Redes Neuronales.
También imprimiremos su valor al llegar
a la última vuelta del "loop" range(5000)
------------------------------------------------
Ejecución bajo consola de linux, con este comando:
python3 derivada_descenso_gradiente_1.py
-------------------------------------------------
***************************************************************
Programa Realizado Bajo plataforma Ubuntu
de linix.
Editado con Sublime text.
También se puede editar y ejecutar con Google Colab
*****************************************
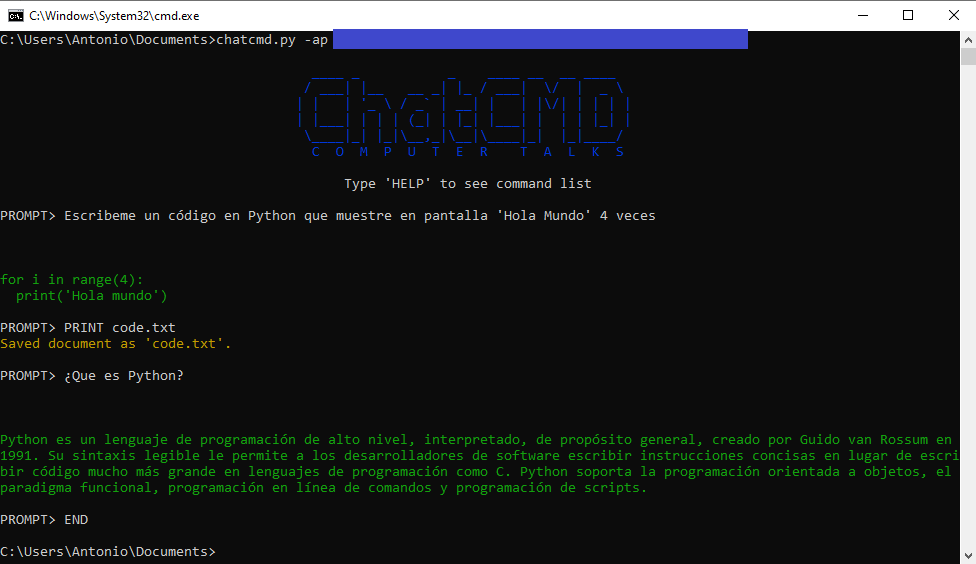
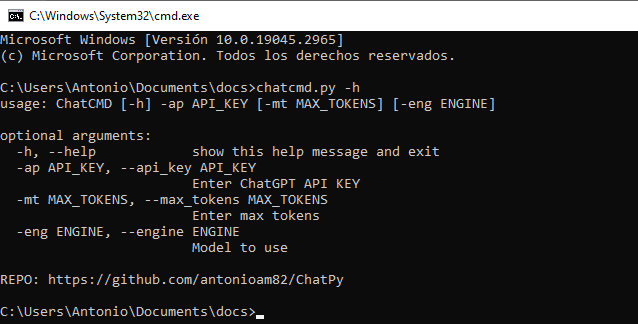
"""Programa para usar ChatGPT dese la terminal. Al iniciarlo se requiere introducir la Api-Key del usuario.
PARA CUALQUIER DUDA U OBSERVACIÓN, USEN LA SECCIÓN DE COMENTARIOS.