Mostrar los tags: r

Les traigo un OCX simple, que les servirá para representar el típico estado On-Off.



Reacciona al hacer un Click sobre el elemento, llamando al Evento Change. Desde ahí capturan el valor (TRUE ó FALSE) y realizar la acción que quieran de acuerdo a éso.

Les adjunto el código fuente, junto al OCX compilado. Espero les sea de utilidad.

El presente programa se encarga de aplicar filtros sobre los fotogramas de un archivo de video empleando diferentes funciones. El programa realiza el filtrado frame a frame para a continuación generar un nuevo video con la secuencia de frames procesados (aplicando el frame rate del vídeo original). También usa el software "ffmpeg" para copiar el audio del vídeo original y añadirlo al vídeo resultante.

USO: Primeramente seleccionaremos el vídeo a filtrar mediante el botón "SEARCH". Una vez seleccionado iniciaremos el proceso con "START FILTERING" con el que empezaremos seleccionando la ubicación del nuevo vídeo, para a continuación iniciar el proceso (NOTA: La ruta del directorio de destino no deberá contener espacios en blanco). El proceso de filtrado podrá ser cancelado medinate el botón "CANCEL".
PARA CUALQUIER DUDA U OBSERVACIÓN USEN LA SECCIÓN DE COMENTARIOS.

Nueva versión del juego de la serpiente con caracteres ASCII. Esta versión se diferencia de las dos anteriores (que pueden verse en mi lista de códigos) en que se acompaña de un archivo (de nombre "hiScore") que irá almacenando de modo permanente, la puntuación máxima alcanzada por el jugador.

BOTONES:
Mover serpiente: Botones de dirección
Pause y reanudar partida pausada : Barra espaciadora.
Finalizar partida en curso: tecla "q"
PARA CUALQUIER PROBLEMA, NO DUDEN EN COMUNICÁRMELO.

********************************************************************************************************************
Aula_18_B.py
******************************************************************************************************************
Se trata de una sencilla red neuronal, ya resuelta en otro ejercicio,
utilizando la librería keras. Ahora lo planteamos de nuevo, utilizando
solamente las librerias numpy y matplotlib.

Se trataba de una red neuronal con este esquema:

input_size = 1
hidden_layer1_size = 8
hidden_layer2_size = 8
output_size = 1


Una neurona de entrada, con dos capas ocultas intermedias de 8 neuronas
cada una, y 1 neurona de salida.

Los datos generales y sencillos de la idea son los siguientes:
Se trata de cinco hermanos que a los 30 años median lo siguiente:
Antonio 1,70 cm. Pedrito 1,75. Juanito 1,78 . Carlitos 1,69. Ignacio 1,87.
Ramón 1,79.
Hace 6 meses ha nacido Santiaguito.
Cuales son las previsiones de estatura
cuando también tenga 30 años. Haremos graficas de salida de columnas.
También haremos gráficas de costos MSE, con salida imprimida por consola
de los valores de los mismos por cada iteración.
También se imprime en la salida la previsión que hace la red neuronal
de la estatura futura

Los hiperparámetros que adoptamos, son los siguientes:
learning_rate = 0.01
epochs = 40

Se puede jugar con los mismos con el fin de afinar los
resultados.
*************************************************************
Este ejercicio ha sido realizado en una plataforma Linux.
Ubuntu 20.04.6 LTS.
Se utiliza el editor Sublime text
*********************************************************
Ejecucion bajo consola linux con el comando:
python3 Aula_18_B.py

python3 Ejercicio_Aula_23_Momentum.py

Sencillo ejercicio sobre un descenso de gradiente con momento, (Gradient Descent with Momentum en inglés).
Se trata de aplicar este algoritmo a una funcion parabolica del tipo: f(x) = x^2 / 6.
Cuya derivada es:x**2 / 6.
El descenso de gradiente con momento es una variante del algoritmo de descenso de gradiente utilizado en la optimización y entrenamiento de modelos de aprendizaje automático, particularmente en el contexto de redes neuronales y problemas de optimización no convexos. Su objetivo es acelerar la convergencia del descenso de gradiente y ayudar a evitar quedarse atrapado en óptimos locales.

La principal diferencia entre el descenso de gradiente con momento y el descenso de gradiente estándar es la adición de un término de "momentum" o impulso. En el descenso de gradiente estándar, en cada iteración, el gradiente actual se utiliza directamente para actualizar los parámetros del modelo. En cambio, en el descenso de gradiente con momento, se mantiene un promedio ponderado exponencial de los gradientes anteriores y se utiliza ese promedio para actualizar los parámetros.

El objetivo del término de momento es suavizar las actualizaciones de los parámetros y reducir las oscilaciones que pueden ocurrir cuando el gradiente varía significativamente en diferentes direcciones. Esto puede ayudar a acelerar la convergencia y a sortear barreras o mínimos locales en la función de costo

En este sencillo ejercicio que propongo, en vez de utilizar datos sintéticos de caráctear aleatorio de entrada, lo vamos a aplicar a una función parabólica.

DesGraMul_Aula_B_228_15_oct_Github.ipynb

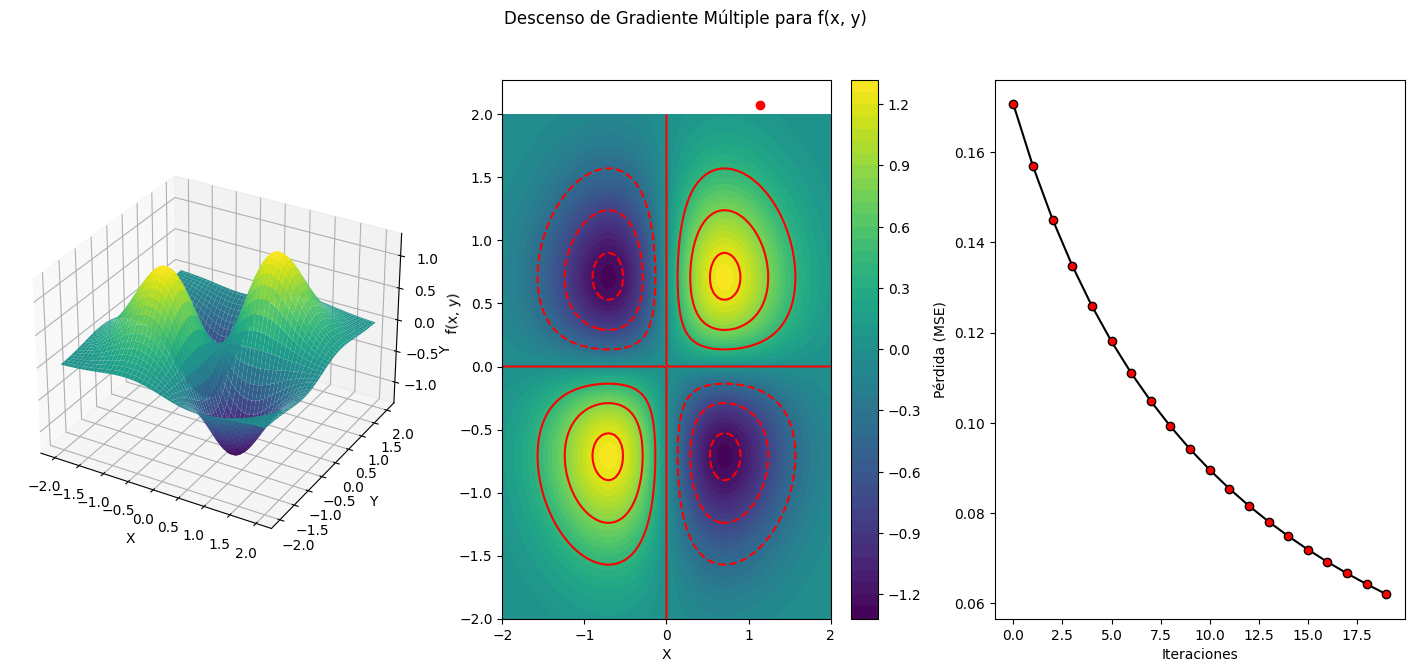
Este ejercicio trata de realizar un descenso de gradiente múltiple en un contexto de gráficos 3D a partir de un punto (x, y) específico. El descenso de gradiente múltiple es una técnica de optimización utilizada para encontrar los mínimos locales o globales de una función multivariable.

Aquí hay una descripción general de cómo puedes abordar este problema:

Función Objetivo: Primero, necesitas tener una función objetivo que desees optimizar en el contexto 3D. Supongamos que tienes una función f(x, y) que deseas minimizar.

Derivadas Parciales: Calcula las derivadas parciales de la función con respecto a x y a y. Estas derivadas parciales te dirán cómo cambia la función cuando modificas x e y.

Punto Inicial: Comienza en un punto (x0, y0) dado. Este será tu punto de inicio.

Tasa de Aprendizaje: Define una tasa de aprendizaje (alfa), que es un valor pequeño que controla cuánto debes moverte en cada iteración del descenso de gradiente. La elección de alfa es crucial y puede requerir ajustes.

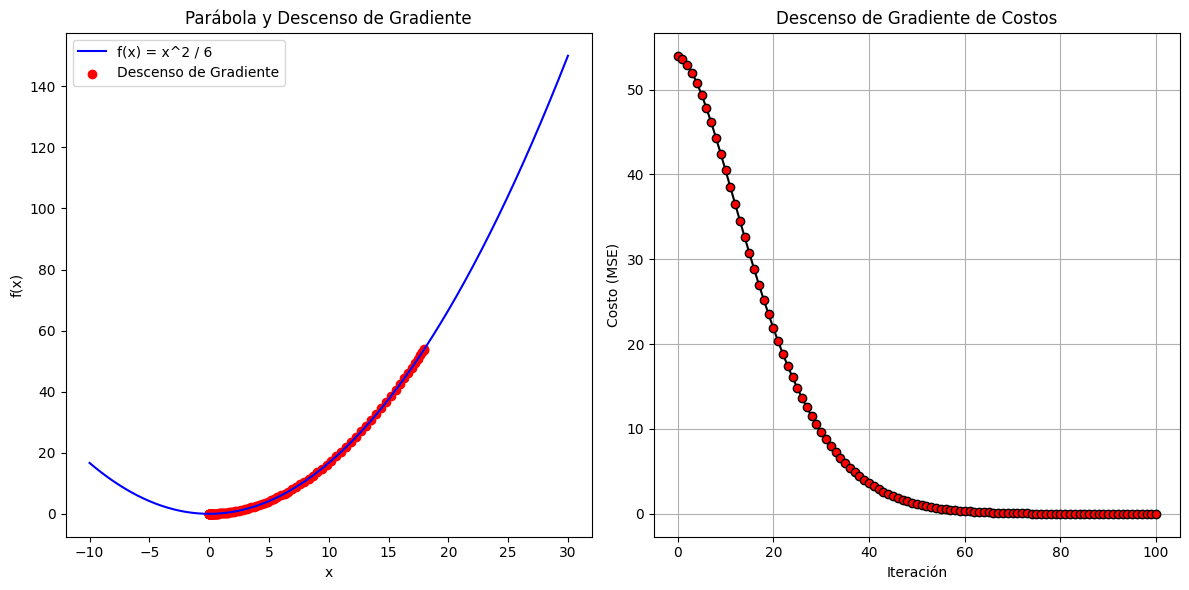
Iteraciones: Itera a través de las siguientes fórmulas hasta que converjas a un mínimo:

Nuevo x: x1 = x0 - alfa * (∂f/∂x)
Nuevo y: y1 = y0 - alfa * (∂f/∂y)

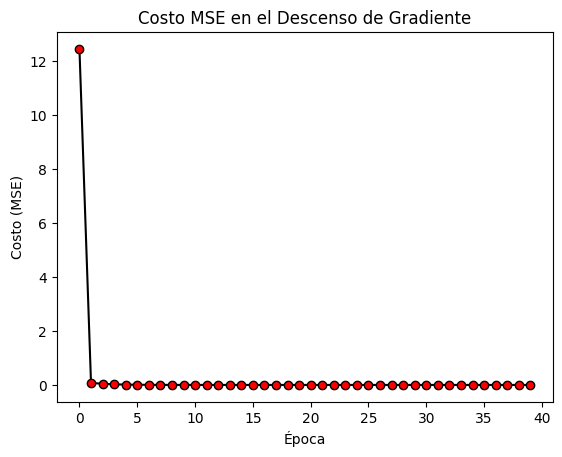
Condición de Parada: Puedes definir una condición de parada, como un número máximo de iteraciones o un umbral de convergencia (por ejemplo, cuando las derivadas parciales son muy cercanas a cero).

Resultados: Al final de las iteraciones, obtendrás los valores de (x, y) que minimizan la función en el contexto 3D.

Es importante recordar que el éxito del descenso de gradiente depende de la elección adecuada de la tasa de aprendizaje, la función objetivo y las condiciones iniciales. Además, en problemas 3D más complejos, es posible que desees considerar algoritmos de optimización más avanzados, como el descenso de gradiente estocástico o métodos de optimización de segundo orden.

Este es un enfoque general para el descenso de gradiente múltiple en un contexto 3D. Los detalles pueden variar según la función objetivo y las necesidades específicas de tu aplicación.