PDF de programación - Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

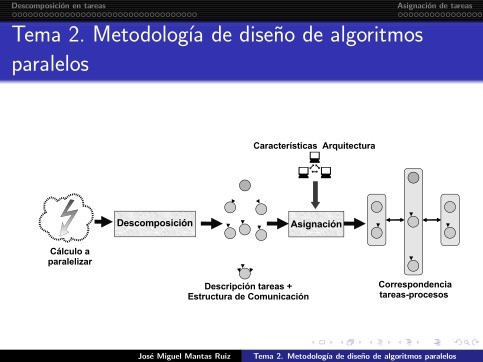
Tema 2. Metodología de diseño de algoritmos
paralelos

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

CONTENIDOS

Asignación de tareas

1 Descomposición en tareas

Conceptos previos
Técnicas de descomposición

2 Asignación de tareas

El problema de la asignación. Objetivos
Estrategias generales
Esquemas de asignación estática
Esquemas de equilibrado dinámico de la carga

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

DESCOMPOSICI ÓN EN TAREAS

Ejemplo: Evaluación polinomial

f i (x) = ai ,0+ai ,1x +. . .+ai ,n−1x n−1+ai ,nx n

,

i = 0, 1, . . . , m−1

Se desea evaluar obtener un v = mínm−1

A =


a0,0
. . .
am−1,0

a0,1
. . .
am−1,1

. . .
. . .
. . .

a0,n
. . .
am−1,n

i =0 f i (b).




José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Granularidad de una descomposición

Tipos de granularidad

Granularidad fina: la descomposición genera un número
elevado de pequeñas tareas.

Granularidad gruesa: se obtienen pocas tareas de gran
tamaño.

Ejemplos

Evaluación de 2000 polinomios
- 500 polinomios por tarea de evaluación: grano grueso (7
tareas).
- 1 polinomio por tarea: grano fino (sobre 4000 tareas):
Suma de vectores. W = U + V , U, V ∈ IRn
- Mínima granularidad aceptable para calcular : Una tarea
separada calcula cada wi

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Grafo de dependencias

Grafo de dependencias

Grafo dirigido acíclico donde los nodos representan tareas y
una arista conectando una tarea fuente con otra destino
representa que para poder ejecutarse la tarea destino debe
ejecutarse previamente la tarea fuente.

Cada nodo del grafo suele etiquetarse con un valor
proporcional al coste computacional de la tarea.

Dependiendo de la estrategia de resolución, se pueden obtener
diferentes grafos.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Grafo de dependencias y grado de concurrencia

Dos grafos de dependencias diferentes que resuelven el mismo
problema

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Grafo de dependencias y grado de concurrencia

Grado de concurrencia

Máximo grado de concurrencia: Mayor número de tareas
cuya ejecución se podría realizar al mismo tiempo en el grafo
de dependencias.

Camino crítico Camino más largo en el grafo desde un nodo
de comienzo hasta un nodo de finalización. La longitud L se
obtiene sumando los costes de los nodos componentes.

Grado medio de concurrencia: Número medio de tareas que
se podrían ejecutar en paralelo, considerando todas las fases
del algoritmo. Para un grafo con N nodos:

M = PN

i =1 coste(nodoi )

L

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Grafo de dependencias y grado de concurrencia

Grado medio de concurrencia para dos grafos de dependencias

M(grafo(a)) =

23
7

= 3.28

M(grafo(b)) =

23
8

= 2.875

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Comunicación y sincronización. Estructura de
comunicación

Estructura de comunicación

Existen relaciones de sincronización y comunicación entre las
tareas que no tienen por qué aparecer en el grafo.

Estructura de comunicación: los nodos representan tareas,
mientras las aristas conectan tareas entre las que existe una
relación de comunicación o sincronización.

Los nodos se etiquetan con valor proporcional a la carga
computacional y las aristas con valores proporcionales a la
cantidad de datos que se comunican.

En muchos casos las aristas son dirigidas para indicar el
sentido del flujo de datos.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Comunicación y sincronización. Estructura de
comunicación

Estructura de comunicación con paso de mensajes

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Fase de descomposición: Visión global

Resultado de la fase de descomposición

Obtiene un conjunto de tareas, junto con una descripción de
su estructura de comunicación que exhibe un grado de
concurrencia alto.

Describe un algoritmo paralelo ideado para una máquina con
un número ingente de procesadores capaces de interactuar
entre sí sin apenas sobrecarga.

Esta solución algorítmica será evaluada y restringida a una
arquitectura particular en la fase de asignación.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Técnicas de Descomposición

Métodos para descomponer la resolución de un problema

Generales

Descomposición de dominio.
Descomposición funcional.
Descomposición recursiva.

Específicos

Descomposición exploratoria.

Mixtos: Combinación de los anteriores.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición de Dominio

Se utiliza cuando es posible resolver un problema aplicando la
misma operación sobre partes diferentes de su dominio de datos.

Fases

a) Se trocean los datos de forma homogénea para obtener

particiones del dominio original.

b) Se estudia cómo asociar computación a cada subdominio de

datos.

c) Se asocia la gestión de cada partición a una tarea que

contendrá los datos y un conjunto de operaciones sobre dichos
datos.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición de Dominio

Datos a descomponer

a) Datos de salida: cada componente de los datos de salida se

puede calcular de forma independiente del resto.

b) Datos de entrada

c) Datos intermedios: es posible a veces obtener un mayor

grado de concurrencia centrándose en datos intermedios entre
etapas.

Consejos

Centrarse primero en la estructura de datos más grande o en
la más usada, analizando distintas posibilidades.

Regla del propietario: Casos a) y b).
La tarea propietaria se encarga de los cálculos ligados a su
subdominio.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición centrada en los datos de salida

Transformación iterativa de un vector
i + x (k)
i −1 − x (k)
x (k)
2

x (k+1)
i

=

i +1

,

i = 0, . . . , n − 1 ,

−1 = x (k)
x (k)
n−1,

n = x (k)
x (k)

0

.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición centrada en los datos de salida

Asignamos porciones disjuntas de elementos consecutivos del
vector de salida a cada tarea

Tarea i(Bloque )

Para k= 0 hasta numero iteraciones hacer

Envia(Bloque[0], (i − 1) mod p);
Envia(Bloque[n/p − 1], (i + 1) mod p);
Recibe(izquierda, (i − 1) mod p);
Recibe(derecha, (i + 1) mod p);
Para j= 0 hasta n/p − 2 hacer

tmp=Bloque[j];
Bloque[j]=(izquierda − Bloque[j] + Bloque[j + 1])/2;
izquierda=tmp;

Bloque[n/p − 1]=(izquierda − Bloque[n/p − 1] + derecha)/2;

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición centrada en los datos de salida

Patrón de comunicación en cada iteración

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición centrada en los datos de entrada

Producto escalar de dos vectores

X = (x0, x1, . . . , xn−1),

Y = (y0, y1, . . . , yn−1),

Z = X · Y = x0y0 + x1y1 + . . . + xn−1yn−1

Descomposición razonable: asignar aproximadamente el mismo
número de elementos de X y de Y a cada tarea, alineando.

Tarea i (i = 0, 1, . . . , p − 1) gestiona bloque de X e Y

Zi =

(i +1)n/p

Xj=in/p

xj yj .

Suma de valores locales: descomposición recursiva.

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición de Algoritmos matriciales por bloques

Multiplicación matriz-vector por bloques

A = (ai ,j ) ∈ IRn×n, x = [ˆx0, . . . , ˆxn−1]T ∈ IRn×1.

y = [ˆy0, . . . , ˆyn−1]T = Ax,

ˆyi =

ai ,j ˆxj .

n−1

Xj=0

Formulación por bloques:
Sea m tal que n es divisible entre m.
A = (Aij ) matriz m × m de submatrices n
x = [x0, . . . , xm−1]T donde cada xi es un subvector n

m × n
m .

m × 1.

yi =

m−1

Xj=0

Ai ,j xj .

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición de Algoritmos matriciales por bloques

Descomposición de la multiplicación matriz-vector por bloques

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición centrada en los datos intermedios

Descomposición de la multiplicación matriz-vector

José Miguel Mantas Ruiz

Tema 2. Metodología de diseño de algoritmos paralelos

Descomposición en tareas

Asignación de tareas

Descomposición funcional dirigida por el flujo de datos

La descomposición se ajusta a la propia arquitectura de la
aplicación a paralelizar.

Pasos

a) Se identifican las partes funcionales del cálculo.

b) Se asigna una tarea para la realización de cada fase

identificada.

c) Se examinan los re