PDF de programación - Práctica 0: Introducción a Matlab

Práctica 0: Introducción a Matlab.

Series Temporales. Diplomatura en Estadística. 2009/2010

Matlab es un programa inicialmente diseñado para realizar operaciones matriciales (MATrix
LABoratory) que ha ido evolucionando hasta convertirse en una herramienta muy utilizada en
distintos campos de la Ingeniería y de las Ciencias en general.

Entorno de ventanas

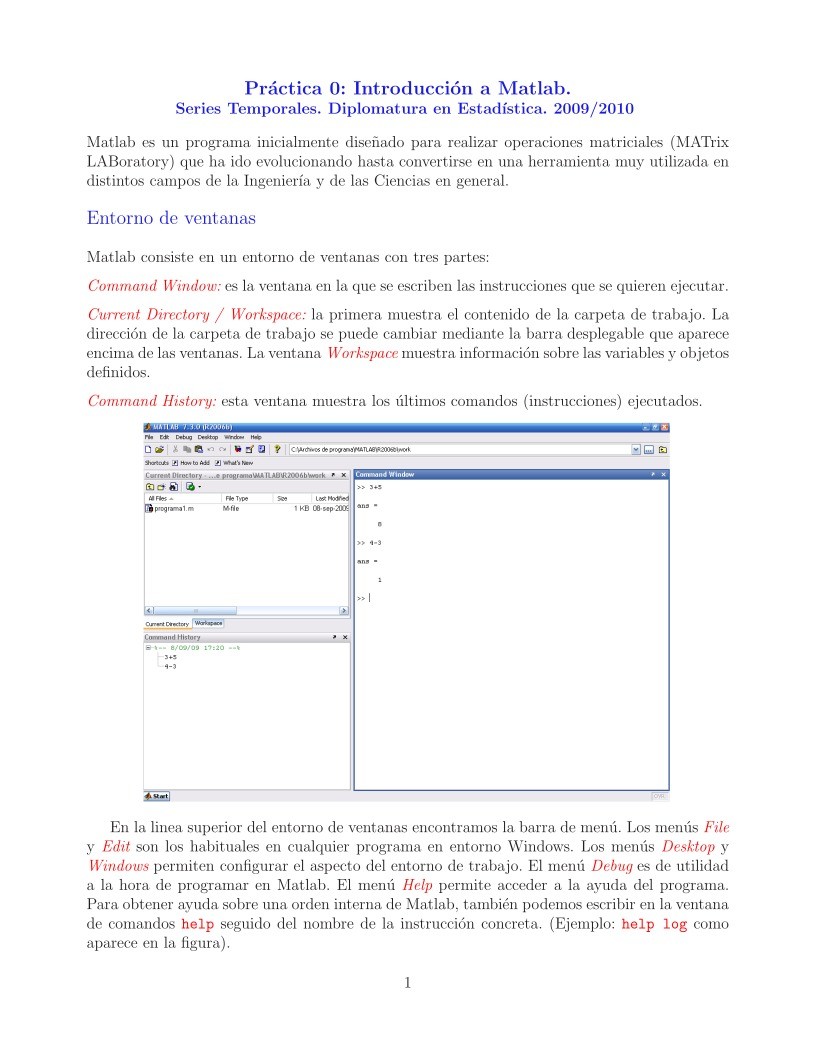
Matlab consiste en un entorno de ventanas con tres partes:

Command Window: es la ventana en la que se escriben las instrucciones que se quieren ejecutar.

Current Directory / Workspace: la primera muestra el contenido de la carpeta de trabajo. La
dirección de la carpeta de trabajo se puede cambiar mediante la barra desplegable que aparece
encima de las ventanas. La ventana Workspace muestra información sobre las variables y objetos
definidos.

Command History: esta ventana muestra los últimos comandos (instrucciones) ejecutados.

En la linea superior del entorno de ventanas encontramos la barra de menú. Los menús File
y Edit son los habituales en cualquier programa en entorno Windows. Los menús Desktop y
Windows permiten configurar el aspecto del entorno de trabajo. El menú Debug es de utilidad
a la hora de programar en Matlab. El menú Help permite acceder a la ayuda del programa.
Para obtener ayuda sobre una orden interna de Matlab, también podemos escribir en la ventana
de comandos help seguido del nombre de la instrucción concreta. (Ejemplo: help log como
aparece en la figura).

1

Comandos básicos

Operaciones aritméticas simples:

>> 2+2
ans =

4

>> 3*2.5
ans =

7.5000

>> 3^2
ans =

9

>> exp(1)
ans =

2.7183

>> log(exp(1))
ans =

>> 4/5
ans =

1

>> log10(10)
ans =

1

>> sin(2*pi)
ans =

-2.4493e-016

>> cos(2*pi)
ans =

1

0.8000
>> 3*(5-1)
ans =

12

>> sqrt(25)
ans =

5

>> 25^(1/2)
ans =

5

>> sqrt(-4)
ans =

0 + 2.0000i

>> real(sqrt(-4))
ans =

0

>> imag(sqrt(-4))
ans =

2

>> 2^(-2)
ans =

0.2500

Obsérvese que las cifras decimales en Matlab se escriben con punto y no con coma.
La sintaxis de las operaciones matemáticas habituales se puede buscar en la ayuda (Help − >
MATLAB Help o directamente apretando la tecla F1).

Para guardar el resultado de una operación en una variable, basta con escribir el nombre de la
variable seguido del signo igual y de la operación que queramos realizar.

>> x=4
x =

2

4

>> y=3+x
y =

7

>> y=y-2
y =

5

>> z=y/2
z =

2.5000

>> who
Your variables are:
ans
>> whos

y

x

z

Name
ans
x
y
z

Size
1x1
1x1
1x1
1x1

Bytes
8
8
8
8

Class
double
double
double
double

Attributes

Las instrucciones who y whos nos dan información sobre las variables definidas. La ventana
Workspace proporciona información adicional sobre las variables.

Podemos eliminar una variable con la instrucción clear.

3

>>clear y
>>who
Your variables are:
ans

x

z

Vectores y matrices

Los vectores se definen como una serie de números entre corchetes, separados por espacios en
blanco o comas.

>> x=[2 3 4]
x =

2

3
>> x=[2,3,4]
x =

2

3

4

4

El vector definido es un vector fila. Podemos transponerlo para obtener un vector columna.

>> xtras=x’
xtras =

2
3
4

Las matrices se definen como una colección de vectores fila de la misma dimensión, separándose
las filas con un punto y coma.

>> M=[2 3 4; 0 -1 0; 1 -2 -1; 3 0 1]
M =

2
0
1
3

3
-1
-2
0

4
0
-1
1

La instrucción size nos da la dimensión de una matriz o vector. La instrucción length nos
da la longitud de un vector, pero no permite saber si se trata de un vector fila o un vector
columna.
>> size(M)
ans =

4

>> size(M’)
ans =

3

>> size(x)
ans =

1

3

4

3

>> size(xtras)
ans =

3

1
>> length(x)
ans =

3

>> length(xtras)
ans =

3

4

Operaciones básicas con vectores y matrices:

>> A=[2 1 -1;0 1 0]
A =

2
0

1
1

-1
0

>> B=[1 3 -1;3 -1 -3]
B =

1
3

3
-1

-1
-3

>> C=[1 1 1; 2 2 2; 1 -1 0]
C =

1
2
1

1
2
-1

1
2
0

>> D=[1 -1; 1 0]
D =

1
1

-1
0
>> E=[1 0 2]
E =

1

0

2

>> A+B %suma de matrices
ans =

3
3

4
0

-2
-3

>> (A+B)*C %suma y producto
ans =

9
0

13
6

11
3

>> A.*B %producto elto. a elto.
ans =

2
0

3
-1

1
0

>> A./B %división elto. a elto.
ans =

2.0000
0

0.3333
-1.0000

1.0000
0

>> 3*A %multiplicación por un escalar
ans =

6
0

3
3

-3
0

>> E/5 %división por un escalar
ans =

0.2000

0

0.4000

>> D^2 %potencia de matrices
ans =

0
1

-1
-1

>> D.^2 %potencia elto. a elto.
ans =

1
1

1
0

>> det(C) %cálculo del determinante
ans =

0

>> D*A %producto matricial
ans =

>> inv(D) %inversa de una matriz
ans =

2
2

0
1

-1
-1

0
-1

1
1

>> C*E’ %producto matricial
ans =

>> inv(A*A’) %inversa de una matriz
ans =

3
6
1

0.2000
-0.2000

-0.2000
1.2000

Nota importante: las operaciones matriciales habituales se representan con los símbolos +,
-, *, ^. Los símbolos .*, .^ , ./ (precedidos por un punto) realizan las operaciones corre-
spondientes elemento a elemento.
Cualquier función matemática definida en Matlab se puede aplicar a una matriz o vector y

5

actúa elemento a elemento.

>> sin(C) %seno de los elementos de C
ans =

0.8415
0.9093
0.8415

0.8415
0.9093
-0.8415

0.8415
0.9093
0

>> log(C) %logaritmo neperiano de los elementos de C
Warning: Log of zero.
ans =

0
0.6931
0

0
0.6931

0 + 3.1416i

0
0.6931
-Inf

>> cos(E*pi) %coseno de los elementos de E multiplicados por pi
ans =

-1

1

1

>> exp(E) %exponencial de los elementos de E
ans =

2.7183

1.0000

7.3891

Notése que el símbolo % se utiliza para escribir comentarios. Cualquier cosa que se escriba
después de % es ignorado por el programa.

Otras formas de definir matrices y vectores:

>> v=[0:1:10] %todos los números del 0 al 10 de 1 en 1
v =

0

1

2

3

4

5

6

7

8

9

10

>> w=[0:0.1:0.5] %todos los números del 0 al 0.5 de 0.1 en 0.1.
w =

0

0.1000

0.2000

0.3000

0.4000

0.5000

>> z=linspace(0,5,10) %un vector de 10 puntos equiespaciados entre 0 y 5
z =

Columns 1 through 7

0

0.5556

1.1111

1.6667

2.2222

2.7778

3.3333

Columns 8 through 10

3.8889

4.4444

5.0000

>> z=linspace(0,5,11) %lo mismo pero con 11 puntos
z =

Columns 1 through 7

0

0.5000

1.0000

1.5000

2.0000

2.5000

3.0000

Columns 8 through 11

3.5000

4.0000
>> A=[0 2 3; 1 1 -1]
A =

0
1

2
1

3
-1

4.5000

5.0000

6

>> a=[0 1 0] %Matlab distingue entre mayúsculas y minúsculas
a =

0

1

0

>> A=[A;a] %añadimos a la matriz A el vector a como última fila
A =

0
1
0

2
1
1

3
-1
0

>> A=[A,a’] %añadimos a la nueva matriz A el vector a como última columna
A =

0
1
0

2
1
1

3
-1
0

0
1
0

>> a=[a 0:1:3] %añadimos al vector a las cifras del 0 al 3
a =

0

1

0

0

1

2

3

Algunas matrices usuales:

>> eye(4) %matriz identidad
ans =

1
0
0
0

0
1
0
0

0
0
1
0

0
0
0
1

>> ones(3) %matriz de unos cuadrada
ans =

1
1
1

1
1
1

1
1
1

>> ones(3,2) %matriz de unos rectangular
ans =

1
1
1

1
1
1

>> zeros(2) %matriz de ceros cuadrada
ans =

0
0

0
0

>> zeros(1,5) %matriz de ceros rectangular
ans =

0

0

0

0

0

Acceder a elementos y submatrices de una matriz:

>> B=[5 1 -5; 3 2 1; 0 1 7]

7

B =

5
3
0

1
2
1

-5
1
7

>> b32=B(3,2) %elemento 3,2 de B
b32 =

1

>> b13=B(1,3) %elemento 1,3 de B
b13 =

-5

>> b1=B(1,:) %primera fila de B (1a fila, todas las columnas)
b1 =

5

1

-5

>> B(1,2:3) %segundo y tercer elementos de la primera fila de B
ans =

1

-5

>> B(2:3, 2:3) %submatriz de B con las filas 2,3 y las columnas 2,3
ans =

2
1

1
7

>> b2c=B(:,2) %segunda columna de B (todas las filas, 2a columna)
b2c =

1
2
1

>> b2c(3) %tercer elemento del vector b2c
ans =

1

>> diag(B) %diagonal de B
ans =

5
2
7

>> d=[1 2 3 4 5]
d =

1

2

3

4

5

>> diag(d) %matriz diagonal con el vector d en la diagonal
ans =

1
0
0
0
0

0
2
0
0
0

0
0
3
0
0

0
0
0
4
0

0
0
0
0
5

>> diag(diag(B)) %matriz diagonal cuya diagonal es la diagonal de B
ans =

8

5
0
0

0
2
0

0
0
7

Obsérvese que la diag tiene dos funciones diferentes dependiendo del tipo de argumento.

Gráficos

La instrucción plot nos permite representar los valores de un vector.

>> x=[0:0.01:1];
>> plot(x)

produce el gráfico de la derecha. Se represen-
tan los valores de x frente al número de compo-
nentes del vector.
Obsérvese que el punto y coma después de una
instrucción hace que no se muestre el resultado
de la misma.

>> y=sin(2*pi*x);
>> plot(x,y, ’r:’)

produce una ventana con el gráfico de la
derecha. Se representan los valores de y
(sen(2πx, x ∈ [0, 1]) frente al vector x.
La opción ’r:’ produce una linea roja (r)
punteada (:). Otras opciones para la instruc-
ción plot aparecen ejecutando la ayuda (help
plot).

>> z=cos(2*pi*x);
>> hold on
>> plot(x,z)

produce el gráfico de la derecha en la misma
ventana que el anterior. La instrucción hold on
permite hacer un hacer un gráfico sobre otro
anterior sin borrar éste. Sin esta instrucción, el
gráfico anterior habría desaparecido. La instruc-
ción hold off produce el efecto contrario.

La instrucción figure crea una nueva ventana gráfica en la que se representarán los gráficos
que se realicen a continuación.

9

Ficheros .m

Podemos escribir las instrucciones que queremos ejecutar en un fichero de Matlab con extensión
.m. De esta forma no tendremos que repetir las instrucciones en la ventana de comandos y
podremos guardar el trabajo. En el menú File podemos crear un nuevo archivo .m, abriendo de
esta forma el editor de archivos de Matlab.

El código del archivo .m se ejecuta escribiendo el nombre del archivo en la ventana de comandos.
Para que Matlab encuentre el archivo, debemos situarnos en la carpeta en la que está guardado
dicho archivo (con la barra de dirección que se encuentra sobre la ventana de comandos).

10

Programación en Matlab

Para programar en Matlab crearemos un archivo .m en el que escribiremos el código. El lenguaje
de Matlab admite las estructuras de programación usuales (if, for, while, ...).

Un ejemplo:

% Programa que calcula la suma de los 100 primeros números.
suma=0;
for i=1:100

%ponemos el contador a 0
%para i=1,...,100

suma=suma+i; %sumamos i al resultado anterior

end
%
%Otra forma de hacerlo.
suma=0;
i=