PDF de programación - Tema 4. Recursividad

Universidad Politécnica de Madrid
Escuela Técnica Superior de Ingeniería de Sistemas Informáticos

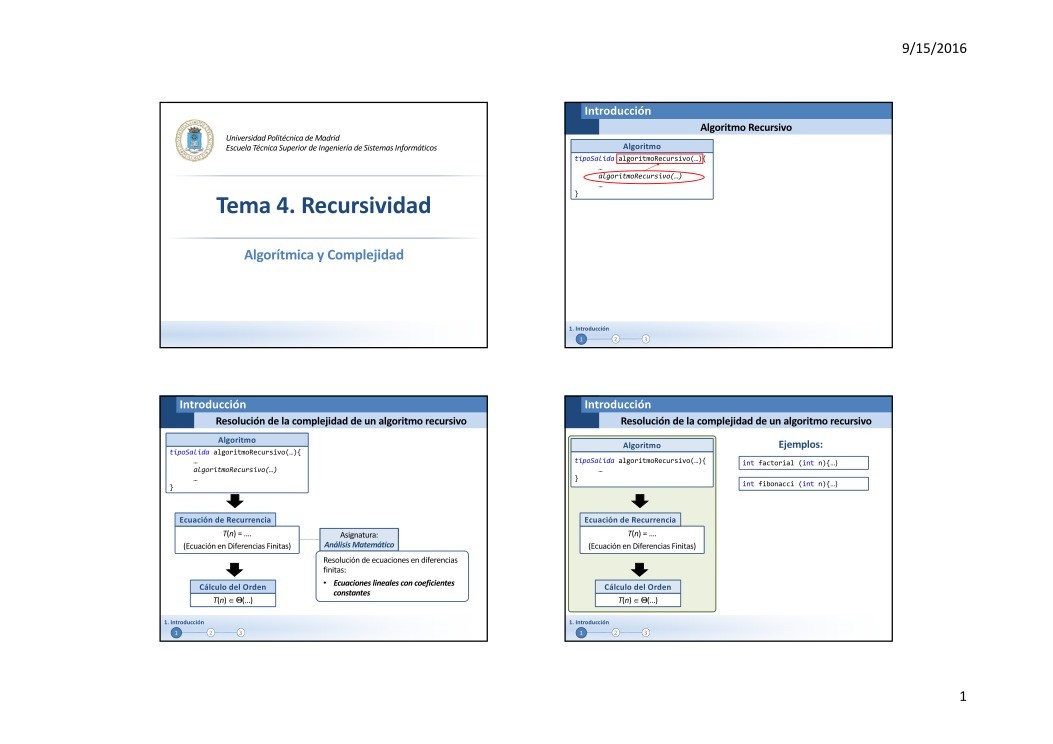
Introducción

Algoritmo

Algoritmo Recursivo

Tema 4. Recursividad

}

Algorítmica y Complejidad

tipoSalida algoritmoRecursivo(…){

…
algoritmoRecursivo(…)
…

Introducción

Resolución de la complejidad de un algoritmo recursivo
Algoritmo

tipoSalida algoritmoRecursivo(…){

…
algoritmoRecursivo(…)
…

}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Asignatura: 

Análisis Matemático
Resolución de ecuaciones en diferencias 
finitas:
• Ecuaciones lineales con coeficientes 

constantes

1. Introducción

1
1

2

3

Introducción

Resolución de la complejidad de un algoritmo recursivo

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ejemplos:

int factorial (int n){…}

int fibonacci (int n){…}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

9/15/2016

1

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ejemplo: factorial

Ejemplos:

int factorial (int n){…}

int fibonacci (int n){…}

9/15/2016

Ejemplo: factorial

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

return n* factorial(n‐1);

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

Ejemplo: factorial

Ejemplo: factorial

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

return n* factorial(n‐1);

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

a  (1)

return n* factorial(n‐1);

Ecuación de Recurrencia



0

1 0

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia



0
1 0

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

2

Ejemplo: factorial

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

T(n‐1)

return n* factorial(n‐1);
T(n ‐ 1) + b

(1)

0

1 0



Ecuación de Recurrencia

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

Ejemplo: factorial

9/15/2016

Ejemplo: factorial

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

return n* factorial(n‐1);

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

Ecuación de Recurrencia



0
1 0

Condiciones 

iniciales

Ejemplo: factorial

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

return n* factorial(n‐1);

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

return n* factorial(n‐1);

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Ecuación de Recurrencia

1

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia

1

Ecuación lineal con coeficientes constantes

Resolución de ecuaciones en 

diferencias finitas 

3

9/15/2016

Ejemplo: factorial

Ejemplos:

int factorial (int n){…}
int factorial (int n){…}

int fibonacci (int n){…}
int fibonacci (int n){…}

Introducción

Algoritmo

Ejemplo: factorial

tipoSalida algoritmoRecursivo(…){

…

}

}

int factorial (int n){

if (n==0)

return 1;

else 

return n* factorial(n‐1);

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Ecuación de Recurrencia

1

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

T(n) = b∙n + a  (n)

Ejemplo: Fibonacci

tipoSalida algoritmoRecursivo(…){

…

}

int fibonacci (int n){
if (n<=1)

return 1;

else 

return fibonacci(n‐1)+fibonacci(n‐2);

}

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ejemplo: Fibonacci

int fibonacci (int n){
if (n<=1)

return 1;

else 

return fibonacci(n‐1)+fibonacci(n‐2);

}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia



1
1 2 0



4

Ejemplo: Fibonacci

Ejemplo: Fibonacci

9/15/2016

T(n‐2)

int fibonacci (int n){
if (n<=1)

return 1;

T(n‐1)

else 

}

return fibonacci(n‐1)+fibonacci(n‐2);

T(n ‐ 1) + T(n ‐ 1) + b

(1)

1
1 2 1



Ecuación de Recurrencia

Ejemplo: Fibonacci

int fibonacci (int n){
if (n<=1)

return 1;

else 

return fibonacci(n‐1)+fibonacci(n‐2);

}

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

int fibonacci (int n){
if (n<=1)

return 1;

else 

a  (1)

return fibonacci(n‐1)+fibonacci(n‐2);

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ecuación de Recurrencia



1
1 2 0



Ejemplo: Fibonacci

int fibonacci (int n){
if (n<=1)

return 1;

else 

return fibonacci(n‐1)+fibonacci(n‐2);

}

}

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ecuación de Recurrencia



Condiciones 

1
1 2 0

iniciales



Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Ecuación de Recurrencia

1 2

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

5

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ejemplo: Fibonacci

int fibonacci (int n){
if (n<=1)

return 1;

else 

return fibonacci(n‐1)+fibonacci(n‐2);

}

9/15/2016

Ejemplo: Fibonacci

int fibonacci (int n){
if (n<=1)

return 1;

else 

return fibonacci(n‐1)+fibonacci(n‐2);

}

Introducción

Algoritmo

tipoSalida algoritmoRecursivo(…){

…

}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia

1 2

Ecuación lineal con coeficientes constantes

Resolución de ecuaciones en 

diferencias finitas 

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

Ecuación de Recurrencia

1 2



1 52

Θ

c1>0

Introducción

Algoritmo

Ecuaciones de Recurrencias

tipoSalida algoritmoRecursivo(…){

…

}

Ecuación de Recurrencia

T(n) = ….

(Ecuación en Diferencias Finitas)

Cálculo del Orden

T(n)  (…)

1. Introducción

1
1

2

3

• 1
• (cid:21