Iniciar sesiónCerrar
Correo:
Contraseña:
Entrar
Recordar sesión en este navegador
Iniciar sesiónIniciar sesiónCrear cuentaCrear cuenta
LWP » Código Fuente » Dev - C++ » Código de Dev - C++ - Desarrollo en serie del Coseno en C++

Código de Dev - C++ - Desarrollo en serie del Coseno en C++

Volver
Agregar Código Fuente
<<>>
Imágen de perfil

Desarrollo en serie del Coseno en C++gráfica de visualizaciones


Dev - C++

Publicado el 3 de Junio del 2021 por Administrador (718 códigos)
2.031 visualizaciones desde el 3 de Junio del 2021
El desarrollo en serie del coseno tiene la forma que se señala a continuación:

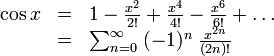
coseno


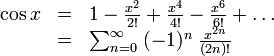
Como puede observarse, es una sucesión infinita de términos de un polinomio de grado n cuyos coeficientes guardan una relación predecible matemáticamente. Los coeficientes con las potencias impares X, X3, X5, X7, …, son todos iguales a cero por lo que no revestiría mayor dificultad generarlos dentro del programa. Por otra parte, los coeficientes de las potencias pares X2, X4, X6, X8, …, se hacen alternadamente negativos para los n/2 impares (1, 3, 5, …) por lo cual tampoco sería un problema generarlos. En definitiva, la evaluación de la función coseno en cualquier punto de su dominio real, expresada como serie de potencias, sería equivalente a evaluar a un polinomio de grado n en el mismo dominio.

Requerimientos

Para ejecutar en la consola de linux:
1
2
g++ coseno.cpp -o coseno
./coseno

201107

Publicado el 3 de Junio del 2021gráfica de visualizaciones de la versión: 201107
2.032 visualizaciones desde el 3 de Junio del 2021
estrellaestrellaestrellaestrellaestrella
estrellaestrellaestrellaestrella
estrellaestrellaestrella
estrellaestrella
estrella


Forma parte de El Blog de José Guerrero
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <iostream>
#include <cstdlib>
#include <iomanip>
 
using namespace std;
 
void evaluapoli(int n, double *f, double x, double &p);
double factorial(int n);
 
int main() {
 
    system ("clear");
 
    int i, n, prod = -1;
 
    //Introduce el grado del polinomio
    cout << "Aproximacion polinomica para el coseno (grado) ? ";
    cin >> n;
 
    double *f;
 
    f = new double [n+1]; // Define el arreglo para los valores de los coeficientes del polinomio
 
    // Se generan los coeficientes del polinomio
    for (i = 0; i <= n; i+=2) {
        prod *= -1;
        f[i] = prod * (1/factorial(i));
    }
 
    for (i = 1; i < n; i+=2) {
        f[i] = 0;
    }
 
    cout << "\n";
    double x, p=0;
 
    cout << "El coseno será evaluado en el punto (radianes)\n\nX ? ";
    cin >> x;
 
    cout << endl;
 
    /* Esta es la función que evalua el polinomio en el punto x. Evita el uso
    de una fórmula con la función pow de la libreria math.h */
    evaluapoli (n, f, x, p);
 
    cout << "Cos(" << x << ") = ";
 
    cout.setf(ios::fixed);
    cout.precision(9);
 
    cout << p << endl;
    cout << endl;
 
    return 0;
 
}
 
void evaluapoli(int n, double *f, double x, double &p) {
 
    int i;
    double *a;
    a = new double [n];
 
    for (i = 0; i <= n; i++) {  // Crea una copia de los elementos de f[i]
                                // porque el ciclo for inferior los destruye
        a[i] = f[i];
    }
 
    for (i = n; i > 0; i--) {
        p = a[i] * x + a[i - 1];
        a[i - 1] = p;
    }
 
    // P es el valor del polinomio en el punto x
}
 
double factorial(int n) {
 
    int i;
    double factor = 1;
 
    for (i = n; i >= 1; i--) {
        factor *= i;
    }
    return factor;
}



Comentarios sobre la versión: 201107 (0)


No hay comentarios
 

Comentar la versión: 201107

Nombre
Correo (no se visualiza en la web)
Valoración
Comentarios...
CerrarCerrar
CerrarCerrar
Cerrar

Tienes que ser un usuario registrado para poder insertar imágenes, archivos y/o videos.

Puedes registrarte o validarte desde aquí.

Codigo
Negrita
Subrayado
Tachado
Cursiva
Insertar enlace
Imagen externa
Emoticon
Tabular
Centrar
Titulo
Linea
Disminuir
Aumentar
Vista preliminar
sonreir
dientes
lengua
guiño
enfadado
confundido
llorar
avergonzado
sorprendido
triste
sol
estrella
jarra
camara
taza de cafe
email
beso
bombilla
amor
mal
bien
Es necesario revisar y aceptar las políticas de privacidad
Acepto las políticas de privacidad

http://lwp-l.com/s7081