Iniciar sesiónCerrar
Correo:
Contraseña:
Entrar
Recordar sesión en este navegador
Iniciar sesiónIniciar sesiónCrear cuentaCrear cuenta
LWP » Código Fuente » Pseudocódigo/Diagramas de Flujo » Código de Pseudocódigo/Diagramas de Flujo - Descomposición en factores primos

Código de Pseudocódigo/Diagramas de Flujo - Descomposición en factores primos

Volver
Agregar Código Fuente
<<>>
Imágen de perfil

Descomposición en factores primosgráfica de visualizaciones


Pseudocódigo/Diagramas de Flujo

Publicado el 27 de Mayo del 2020 por Administrador (718 códigos)
5.248 visualizaciones desde el 27 de Mayo del 2020
Un número primo es un número p>=2p>=2 que tiene únicamente como divisores positivos a 11 y a pp. Los números mayores o iguales a dos que no son primos, son denominados de números compuestos.

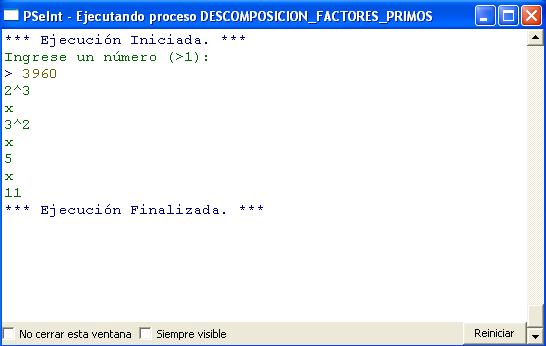
Según la teoría de números, un número compuesto se describir como el producto de dos o más números primos. Estos números primos se denominan factores primos y el proceso de encontrar los factores primos de un número se denomina factorización.

Dado un número natural mayor o igual a dos se pide:
- Representar el número como un producto de sus factores primos.
- Representar el número como un producto de sus factores primos pero en caso que se repita un factor primo, deberá indicarse el exponente de este.

descomposicion-factores-primos

20200502

Publicado el 27 de Mayo del 2020gráfica de visualizaciones de la versión: 20200502
5.249 visualizaciones desde el 27 de Mayo del 2020
estrellaestrellaestrellaestrellaestrella
estrellaestrellaestrellaestrella
estrellaestrellaestrella
estrellaestrella
estrella


Forma parte de Descomposición en factores primos
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
//Creado por Andrés Melgar
//para iterando++ http://iterando.online/
//entrada: http://iterando.online/ejercicios-resueltos/descomposicion-en-factores-primos-en-pseint/
Funcion verifica_si_es_primo <- es_primo(n)
	verifica_si_es_primo <- Verdadero
	Si n<=0 Entonces
		verifica_si_es_primo <- False
	SiNo
		cant_divisores<-0
		encontro_divisores<-Falso
		limite<-trunc(rc(n))
		i<-2
		Mientras i<=limite y no encontro_divisores Hacer
			Si n mod i=0 Entonces
				cant_divisores <- cant_divisores+1
			FinSi
			i<-i+1
		FinMientras
		Si cant_divisores>0  o n=1 Entonces
			verifica_si_es_primo <- False
		FinSi
	FinSi
Fin Funcion
 
Funcion n <- siguiente_primo(n)
	Repetir
		n <- n+1
	Mientras Que no es_primo(n)
Fin Funcion
 
Funcion escribe_factor(hay_factores Por Referencia, factor_primo, cant_factores Por Referencia)
	Si hay_factores Entonces
		Escribir "x"
	SiNo
		hay_factores <- Verdadero
	FinSi
	Si cant_factores=1 Entonces
		Escribir factor_primo
	SiNo
		Escribir factor_primo, "^", cant_factores
	FinSi
	cant_factores <- 0
FinFuncion
 
Funcion descomponer_factores(n)
	productoria <- 1
	copia_n <- n
	factor_primo <- 2
	cant_factores <- 0
	hay_factores<-Falso
	Repetir
		resto <- copia_n mod factor_primo
		Si resto=0 Entonces
			copia_n <- trunc(copia_n/factor_primo)
			productoria<-productoria*factor_primo
			cant_factores <- cant_factores+1
		SiNo
			Si cant_factores > 0 Entonces
				escribe_factor(hay_factores, factor_primo, cant_factores)
			FinSi
			factor_primo <- siguiente_primo(factor_primo)
		FinSi
	Mientras Que productoria<>n
	escribe_factor(hay_factores, factor_primo, cant_factores)
FinFuncion
 
Algoritmo Descomposicion_factores_primos
	Escribir "Ingrese un número (>1): "
	Leer n
	Si n<=1 Entonces
		Escribir "Debe ingresar un número mayor que uno"
	SiNo
		descomponer_factores(n)
	FinSi
FinAlgoritmo



Comentarios sobre la versión: 20200502 (0)


No hay comentarios
 

Comentar la versión: 20200502

Nombre
Correo (no se visualiza en la web)
Valoración
Comentarios...
CerrarCerrar
CerrarCerrar
Cerrar

Tienes que ser un usuario registrado para poder insertar imágenes, archivos y/o videos.

Puedes registrarte o validarte desde aquí.

Codigo
Negrita
Subrayado
Tachado
Cursiva
Insertar enlace
Imagen externa
Emoticon
Tabular
Centrar
Titulo
Linea
Disminuir
Aumentar
Vista preliminar
sonreir
dientes
lengua
guiño
enfadado
confundido
llorar
avergonzado
sorprendido
triste
sol
estrella
jarra
camara
taza de cafe
email
beso
bombilla
amor
mal
bien
Es necesario revisar y aceptar las políticas de privacidad
Acepto las políticas de privacidad

http://lwp-l.com/s6231