"""
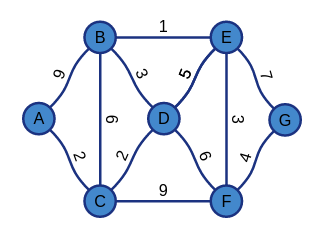
B---1---E
/|\ /|\
9 | 3 5 | 7
/ | \ / | \
A 6 D 3 G
\ | / \ | /
2 | 2 6 | 4
\|/ \|/
C---9---F
"""
import math
# Cada elemento de este diccionario contiene una posicion del camino, y como
# valor tiene una lista con el calculo del camino mas corto, y el origen del
# mismo
valores={ "a":[math.inf,""],
"b":[math.inf,""],
"c":[math.inf,""],
"d":[math.inf,""],
"e":[math.inf,""],
"f":[math.inf,""],
"g":[math.inf,""]
}
# aquí establecemos cada uno de los caminos en una sola dirección y el coste
# que tiene cada camino
caminos=[
["a","b",9],
["a","c",2],
["b","c",6],
["b","e",1],
["c","f",9],
["d","b",3],
["d","c",2],
["d","e",5],
["d","f",6],
["e","f",3],
["e","g",7],
["f","g",4]
]
def setValores(origen,destino,valor):
"""
Función que actualiza el valor del diccionario valores, actualizando
el valor al mas vajo y indicando de de que punto viene el camino mas corto
Tiene que recibir:
origen -> punto inicial
destino -> punto final
valor -> valor de ese tramo + el valor que tiene el origen
Devuelve True o False, dependiendo si ha disminuido el valor entre dos puntos
"""
if valor<valores[destino][0]:
# guardamos el nuevo valor mas bajo
valores[destino][0]=valor
# guardamos de donde viene el valor mas bajo
valores[destino][1]=origen
return True
return False
# definimos el inicio y el destino
inicio="a"
final="g"
valores[inicio][0]=0
# realizamos un bucle hasta que no haya ningun otro cambio de valores
while True:
cancel=True
# recorremos cada uno de los caminos
for i in caminos:
# enviamos los datos del camino
if setValores(i[0],i[1],valores[i[0]][0]+i[2]):
cancel=False
# enviamos los datos del camino de forma invertida
if setValores(i[1],i[0],valores[i[1]][0]+i[2]):
cancel=False
# finalizamos el bucle cuando ya no hay ningun cambio en los valores
if cancel:
break
# iniciamos la busqueda del camino mas corto
camino=[final]
while True:
if camino[-1]==inicio:
break
camino.append(valores[camino[-1]][1])
print("El camino mas corto desde el punto '{}' y el punto '{}' es: {}".format(inicio, final, camino[::-1]))


Comentarios sobre la versión: Versión 1 (4)