"""
**********************************************************
Hilario Iglesias Martínez
**********************************************************
La función sigmoide es una función matemática que toma
cualquier número real como entrada y la transforma en
un valor en el rango de 0 a 1. Su forma característica
es una curva en forma de "S".
La función sigmoide es comúnmente utilizada en diversos campos,
como la biología, la psicología y el aprendizaje automático,
especialmente en las redes neuronales.
Forma:
f(x)=1 / (1 + e**(-x))
Derivada:
e**(-x) / (1 + e**(-x))**2
La función sigmoide toma valores positivos y negativos de
x y los mapea en el rango (0, 1), de modo que valores grandes de
x resultarán en valores cercanos a 1, y valores pequeños o negativos de
x resultarán en valores cercanos a 0.
Programa realizado bajo linux
Plataforma Ubuntu 20.04.6 LTS.
Editado con Sublime Text.
Ejecucion en consola linux.
python3 SigmoideWeb.py
Tambien se puede editar y ejecutar en Google Colab.
"""
import numpy as np
import matplotlib.pyplot as plt
e = 2.71828
# Definimos la función sigmoide y su derivada
def FuncionSigmoide(x):
return 1 / (1 + e**(-x))
def Sigmoid_Derivada(x):
return e**(-x) / (1 + e**(-x))**2
# Creamos un rango de valores a lo largo de la longitud de la función sigmoide
x_rango = np.linspace(-10, 10, 400) # Ajusta el rango según tus necesidades
# Calculamos los valores de la función sigmoide y su derivada en el rango
ValoresSigmoide = FuncionSigmoide(x_rango)
ValoresDerivadaSigmoide = Sigmoid_Derivada(x_rango)
# Parámetros iniciales para el proceso de derivada descendente
x_inicial = 1.0
learning_rate = 0.1
interaciones = 1000
x_historia = [x_inicial]
y_historia = [FuncionSigmoide(x_inicial)]
# Realizar el proceso de derivada descendente
for _ in range(interaciones):
x_inicial = x_inicial - learning_rate * Sigmoid_Derivada(x_inicial)
x_historia.append(x_inicial)
y_historia.append(FuncionSigmoide(x_inicial)) # Corregido aquí
# Detener la iteración si x está cerca de 0
if x_inicial < 0.01:
break
# Corregir la generación del rango de valores para la segunda gráfica
x_rango_Segunda = np.linspace(x_historia[0], x_historia[-1], len(x_historia))
y_rango_Segunda = FuncionSigmoide(x_rango_Segunda)
# Graficar la función sigmoide y el proceso de gradiente descendente
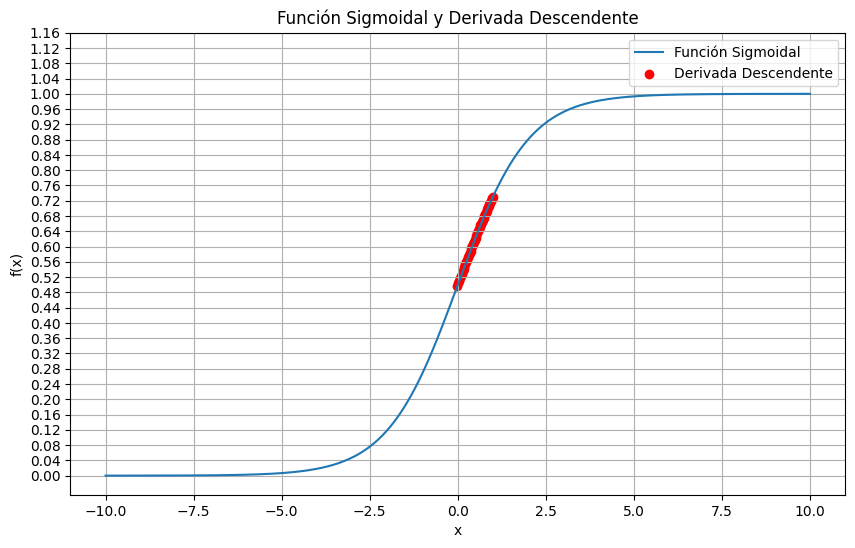
plt.figure(figsize=(10, 6))
plt.plot(x_rango, ValoresSigmoide, label='Función Sigmoidal')
plt.scatter(x_historia, y_historia, color='red', label='Derivada Descendente')
plt.xlabel('x')plt.ylabel('f(x)')plt.title('Función Sigmoidal y Derivada Descendente')plt.grid(True)
plt.legend()
# Agregar divisiones en el eje y
y_ticks = np.arange(0, 1.2, 0.04)
plt.yticks(y_ticks)
plt.show()