**********************************************************************************************
************************************************************************************************
Ejercicio:
Aula_28_Minado_Bitcoin_Target_Marzo_14_25.py
********************************************************
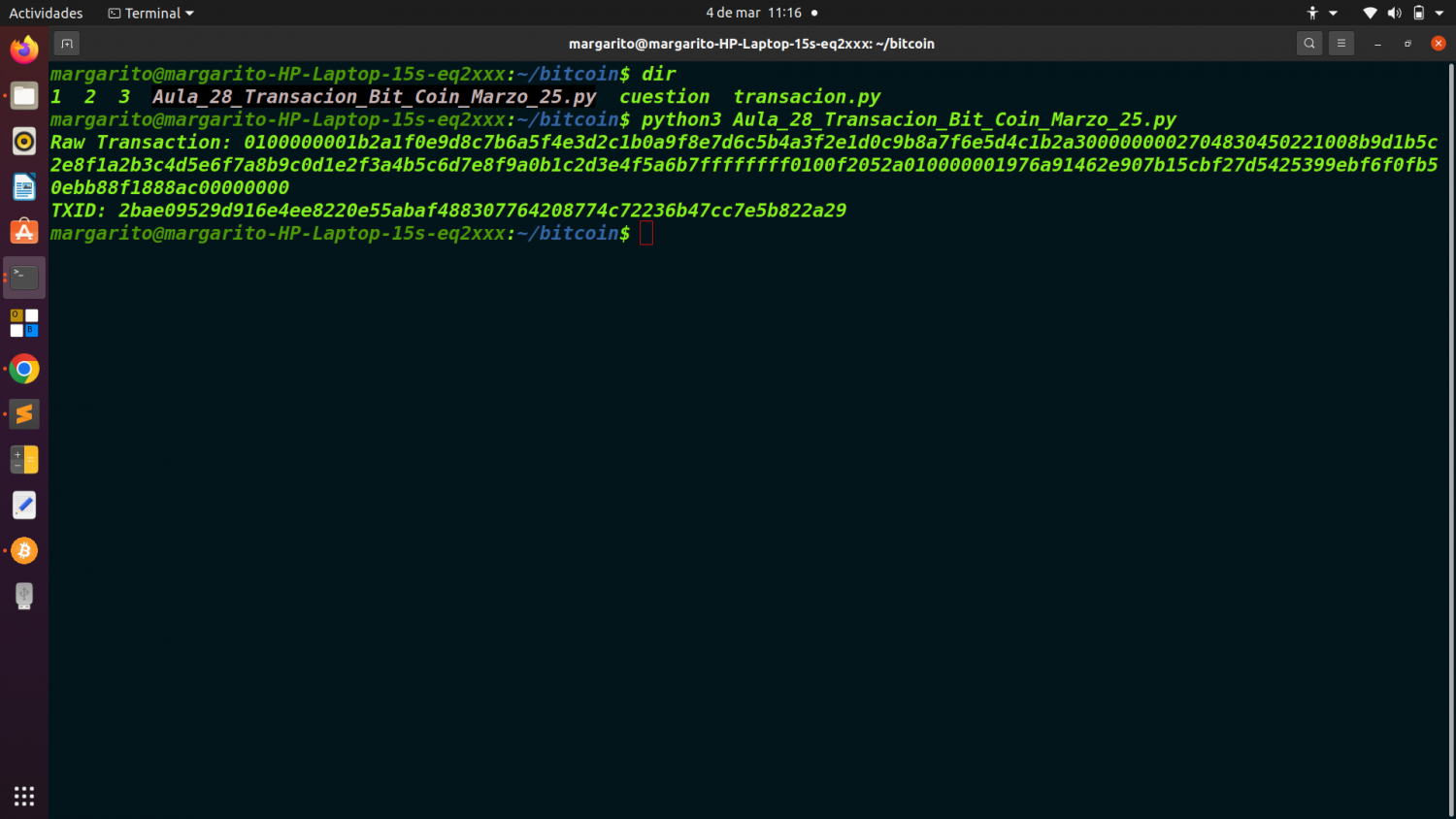
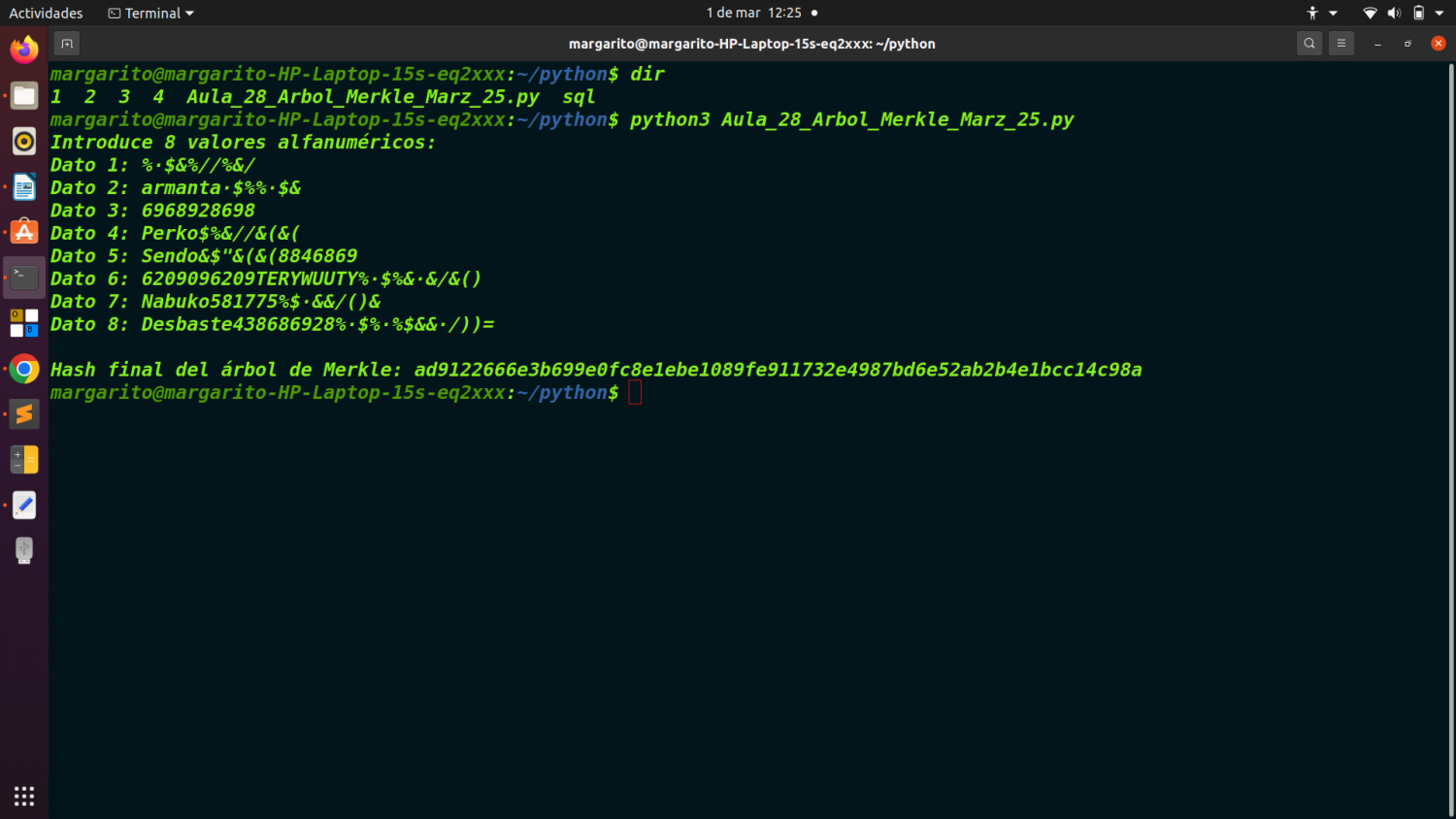
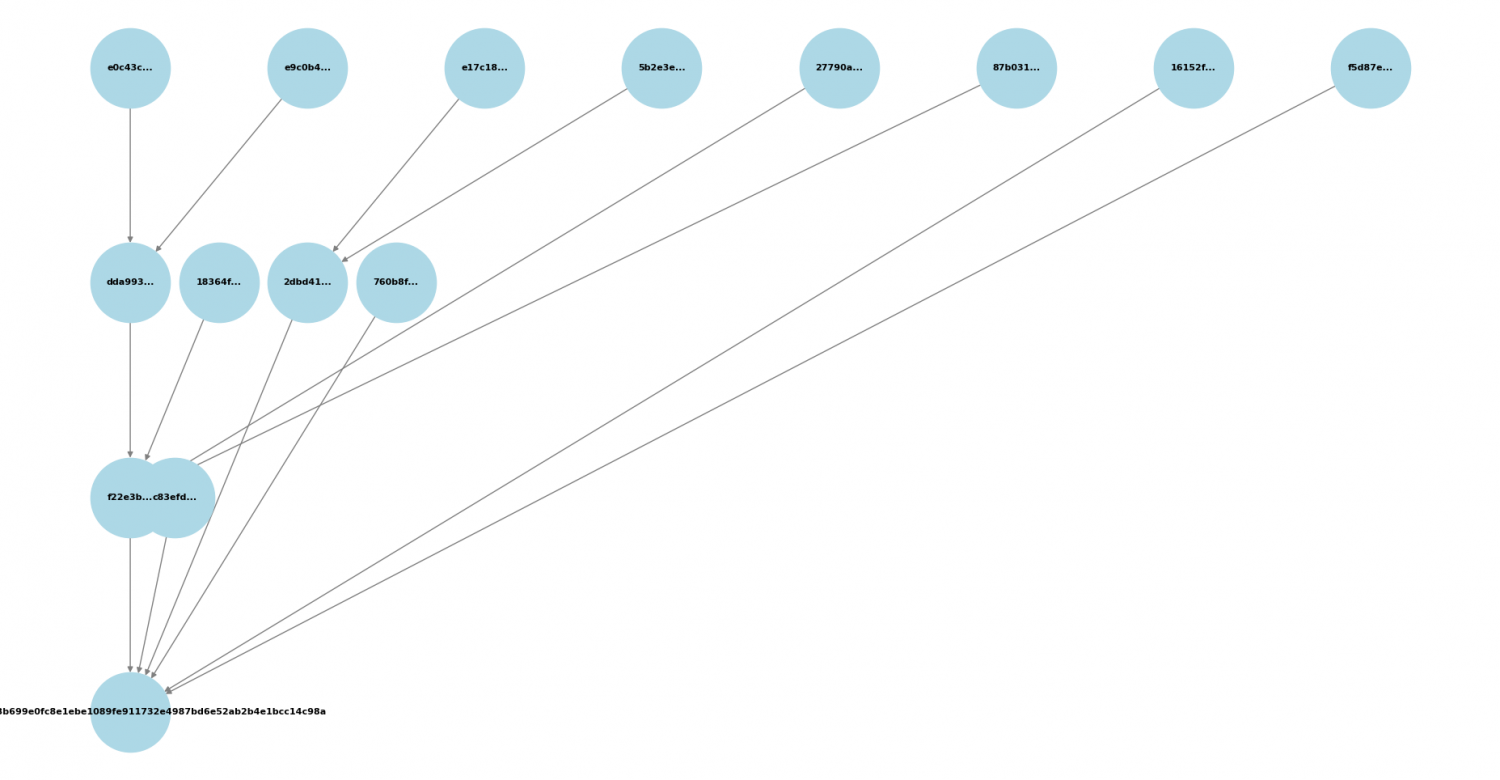
Sobre el bitcoin, habíamos planteado anteriormente dos ejercicios sucesivos sobre arboles de Merkle, y el analisis de una transación de Bitcoins en formato RAW. Hoy propongo para el aula y taller 28, un sencillo ejercicio en Python que tratara sobre em minado de Bitcoins.
En líneas generales el minado de Bitcoin en qué consiste:
****************************************************************
El minado de Bitcoin es el proceso mediante el cual se validan y registran transacciones en la blockchain de Bitcoin, asegurando la red y emitiendo nuevas monedas como recompensa a los mineros. A grandes rasgos, implica lo siguiente:
Agrupación de transacciones en bloques:
-----------------------------------------------------
Los mineros recopilan transacciones pendientes de la mempool (el "pool de memoria" donde se almacenan temporalmente).
Crean un bloque con estas transacciones y añaden un encabezado que incluye el hash del bloque anterior, un marcador de tiempo y otros datos.
Resolución de una prueba de trabajo (PoW - Proof of Work):
Para añadir un bloque a la blockchain, los mineros deben encontrar un hash que cumpla con ciertos requisitos de dificultad.
Esto se hace probando diferentes valores (llamados nonce) y calculando el hash SHA-256 del bloque repetidamente hasta encontrar uno válido.
La dificultad del hash está determinada por el protocolo y se ajusta cada 2016 bloques (~cada dos semanas) para mantener un tiempo promedio de 10 minutos por bloque.
Difusión y validación del bloque:
Cuando un minero encuentra un hash válido, transmite el bloque a la red.
Otros nodos verifican que las transacciones sean legítimas y que la prueba de trabajo sea correcta.
Si el bloque es válido, se añade a la blockchain y la red sigue minando el siguiente bloque a partir de este.
Recompensas por minado:
El minero que resuelve el bloque recibe una recompensa en Bitcoin (actualmente 6.25 BTC por bloque, pero se reduce a la mitad cada 210,000 bloques en el evento llamado halving).
Además, recibe las comisiones de transacción de las operaciones incluidas en el bloque.
En resumen, el minado de Bitcoin es una carrera entre mineros para resolver un problema matemático difícil con fuerza bruta, asegurando la red y permitiendo la emisión controlada de nuevos bitcoins.
Bien, esto que aprimera vista parece un tanto farragoso, lo explicamos en este ejercicio de Python.
QUÉ PARÁMETROS ENTRAN EN EL MINADO:
******************************************************
1. Parámetros técnicos del bloque.
**************************************
Merkle Root: Raíz del árbol de Merkle que agrupa todas las transacciones dentro del bloque.
Versión del bloque: Número que indica la versión del protocolo en uso.
Hash del bloque anterior: Identificador único del bloque anterior en la cadena.
Marca de tiempo (Timestamp): Hora en que se generó el bloque, expresada en segundos desde 1970 (UNIX time).
Bits (Dificultad objetivo): Indica el nivel de dificultad que debe cumplir el hash del bloque.
Nonce: Número aleatorio que los mineros modifican hasta encontrar un hash válido.
2. Parámetros de minado (Prueba de Trabajo - PoW)
************************************************************
Algoritmo de hashing: Bitcoin usa SHA-256 para generar los hashes.
Dificultad de minado: Ajustada cada 2016 bloques (~2 semanas) para que el tiempo promedio de creación de bloques siga siendo 10 minutos.
Objetivo (Target): Límite numérico que el hash del bloque debe cumplir (ser menor que un valor determinado por la dificultad).
Tasa de hash (Hashrate): Velocidad con la que un minero puede calcular hashes por segundo.
Consumo energético: Cantidad de electricidad utilizada por el minero para realizar cálculos.
3. Parámetros económicos.
*******************************
Recompensa por bloque: Actualmente 6.25 BTC, se reduce a la mitad cada 210,000 bloques (halving).
Comisiones de transacción: Pagos que los usuarios adjuntan a sus transacciones para incentivar a los mineros a incluirlas en el bloque.
Costo de hardware: Precio de los equipos de minería, como ASICs especializados.
Costo de electricidad: Factor crucial que afecta la rentabilidad del minero.
4. Parámetros de red.
************************
Mempool: Espacio donde esperan las transacciones antes de ser incluidas en un bloque.
Latencia de red: Velocidad con la que se propagan los bloques en la red, lo que puede afectar la probabilidad de éxito en la minería.
Competencia minera: Cantidad de mineros activos y su potencia de cómputo total en la red (hashrate global).
5. Parámetros de dificultad y ajuste.
****************************************
Retargeting de dificultad: Se ajusta cada 2016 bloques para mantener el tiempo promedio de generación en 10 minutos.
Número de mineros en la red: Mientras más mineros haya, mayor será la competencia y la dificultad.
***************************************************************************************
En nuestro ejercicio, queidos alumnos, nos fijaremos sólo en el punto 1.
Aqui pasamos a describir los pasos de nuestro ejercicio:
-------------------------------------------------------
1. Importación de módulos.
*************************
import hashlib
import time
import struct
hashlib: Para calcular el doble SHA-256, que se usa en la minería de Bitcoin.
time: Para manejar el timestamp y calcular el tiempo transcurrido.
struct: Para empaquetar los datos del bloque en el formato binario usado en Bitcoin.
2. Funciones principales.
*************************
2.1. Cálculo del doble SHA-256.
-----------------------------
def double_sha256(header):
return hashlib.sha256(hashlib.sha256(header).digest()).hexdigest()
Se aplica SHA-256 dos veces al encabezado del bloque, que es el método que usa Bitcoin.
2.2. Conversión de bits a target.
-------------------------------
def bits_to_target(bits):
bits_int = int(bits, 16)
exponent = (bits_int >> 24) & 0xFF
mantissa = bits_int & 0xFFFFFF
target = mantissa * (2 ** (8 * (exponent - 3)))
return hex(target)[2:].zfill(64)
Bitcoin usa una representación compacta de la dificultad llamada bits.
Esta función lo convierte en el valor real del target, que es el número máximo que puede tener un hash válido.
3. Parámetros del bloque.
***********************
version = "0x20000000"
previous_block_hash = "0000000000000000000aef1f5f7de00000000000000000000000000000000000"
merkle_root = "4a5e1e4baab89f3a32518a88c31bc87f00000000000000000000000000000000"
bits = "1E00FFFF" # Se ha aumentado para reducir la dificultad
nonce = 0
timestamp = int(time.time())
version: Versión del protocolo Bitcoin.
previous_block_hash: Hash del bloque anterior.
merkle_root: Raíz del árbol de Merkle (aglutina todas las transacciones).
bits: Representación compacta de la dificultad.
nonce: Número que cambia hasta encontrar un hash válido.
timestamp: Momento en que el bloque fue creado.
4. Creación del encabezado del bloque.
************************************
def create_block_header(version, prev_hash, merkle_root, timestamp, bits, nonce):
return struct.pack("<L32s32sLLL",
int(version, 16),
bytes.fromhex(prev_hash.zfill(64)),
bytes.fromhex(merkle_root.zfill(64)),
timestamp,
int(bits, 16),
nonce)
Empaqueta los datos del bloque en un formato binario para ser minado.
Formato:
<L32s32sLLL
Indica que los datos están en little-endian (el formato usado en Bitcoin).
5. Bucle de minado.
*****************
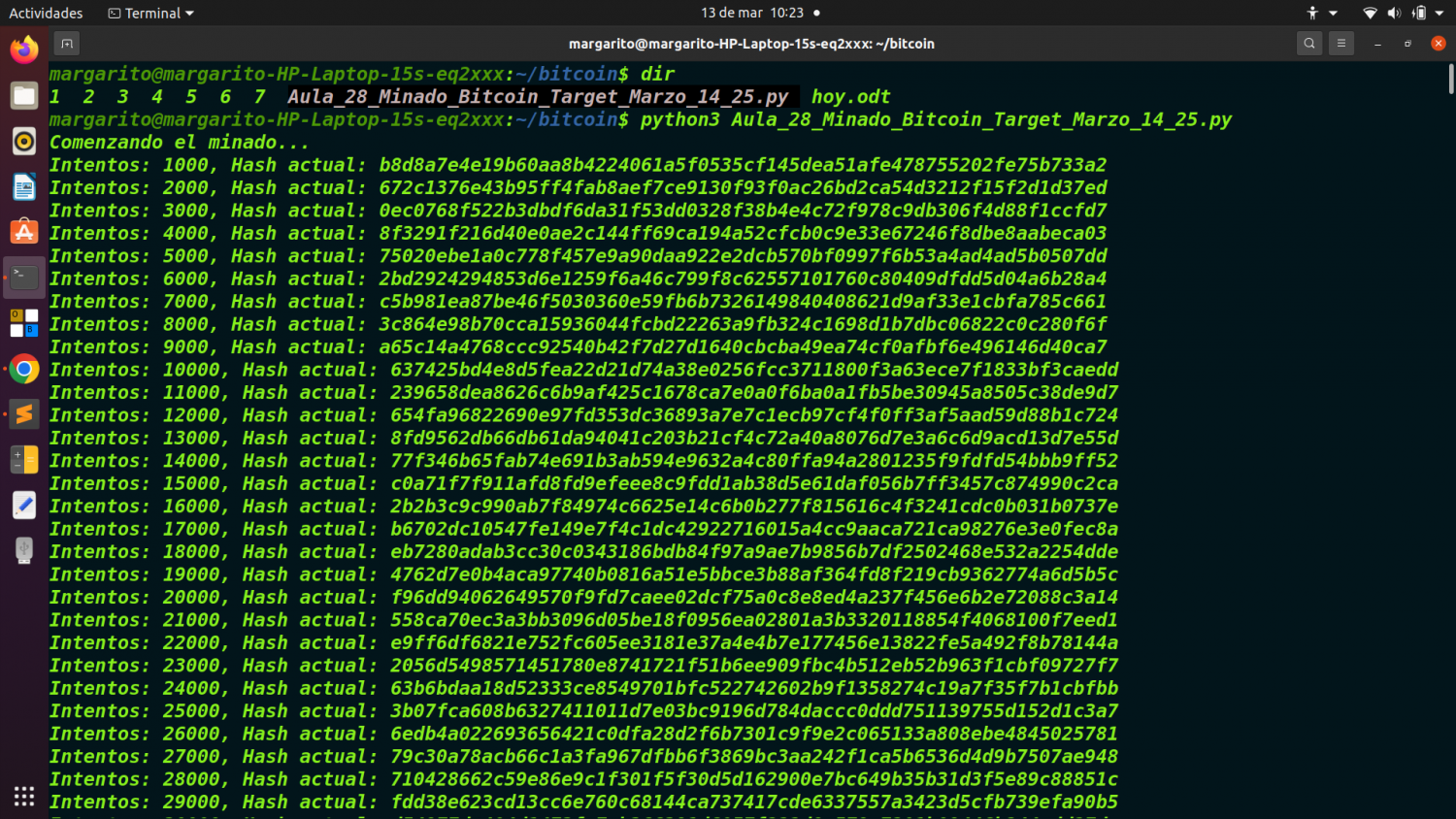
print("Comenzando el minado...")
start_time = time.time()
target_time = 160
Se inicia el minado y se establece un límite de tiempo para evitar que el código corra indefinidamente.
while True:
elapsed_time = time.time() - start_time
if elapsed_time > target_time:
print(f"Tiempo límite alcanzado ({target_time} segundos). Minado detenido.")
break
Si el tiempo excede target_time, se detiene la minería.
5.1. Creación del bloque y cálculo del hash.
******************************************
block_header = create_block_header(version, previous_block_hash, merkle_root, timestamp, bits, nonce)
block_hash = double_sha256(block_header)
Se genera el encabezado del bloque y se calcula su hash con doble SHA-256.
5.2. Verificación del hash.
**************************
if int(block_hash, 16) < int(target, 16):
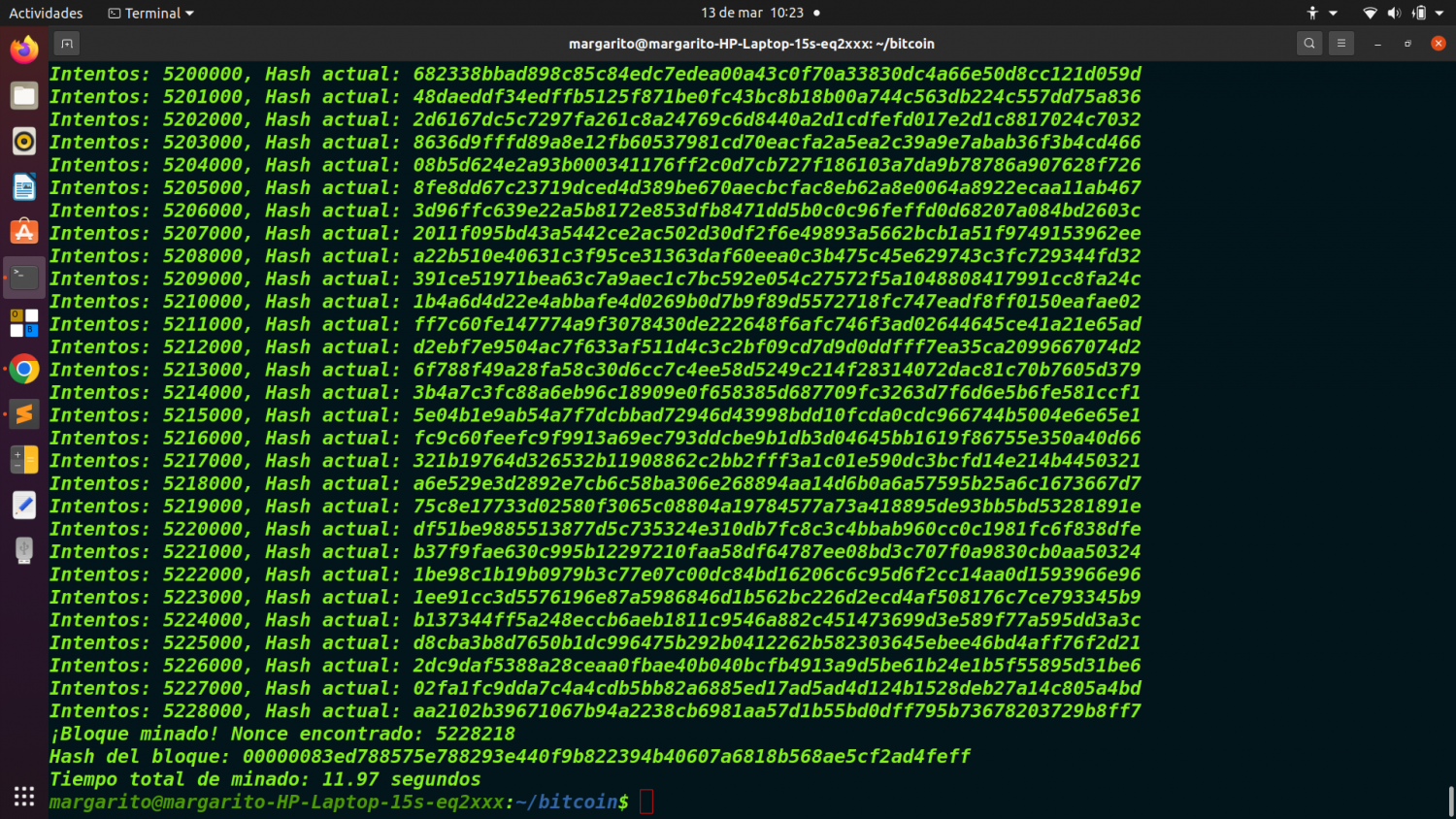
print(f"¡Bloque minado! Nonce encontrado: {nonce}")
print(f"Hash del bloque: {block_hash}")
break
Si el hash generado es menor que el target, significa que el bloque ha sido minado con éxito.
Se imprime el nonce encontrado y el hash válido del bloque.
5.3. Incremento del nonce.
*************************
nonce += 1
Si el hash no es válido, se incrementa el nonce y se prueba de nuevo.
5.4. Mostrar progreso.
*********************
if nonce % 1000 == 0:
print(f"Intentos: {nonce}, Hash actual: {block_hash}")
Cada 1,000 intentos imprime el hash actual para ver el progreso del minado.
6. Impresión de estadísticas finales.
***********************************
end_time = time.time()
print(f"Tiempo total de minado: {end_time - start_time:.2f} segundos")
Muestra el tiempo total que tardó en encontrar el nonce correcto.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Este ejercicio, fue realizado sobre plataforma Linux.
Ubuntu 20.04.6 LTS.
Editado, con Sublime text.
Ejecutado bajo consola Linux, con este comando:
python3 Aula_28_Minado_Bitcoin_Target_Marzo_14_25.py





 (2)
(2)