PDF de programación - Números y hoja de cálculo VI

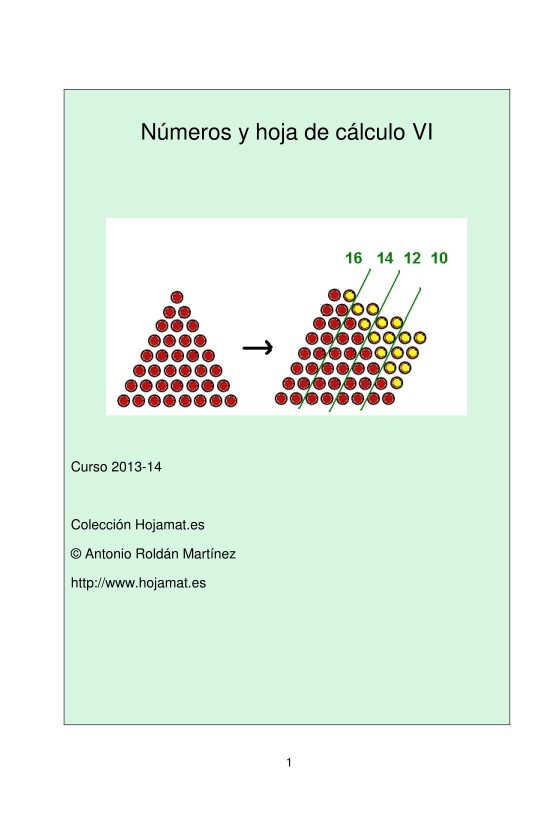
Números y hoja de cálculo VI



Curso 2013-14



Colección Hojamat.es

© Antonio Roldán Martínez

http://www.hojamat.es



1





PRESENT ACIÓN

Llegamos al sexto volumen de los resúmenes anuales del blog
“Números y hoja de cálculo” con la apertura de nuevos temas que
continuaremos en un futuro.

El primero, de las sucesiones recurrentes de segundo orden ha
constituido todo un ciclo, en el que hemos presentado los ejemplos
más representativos, salvo la de Fibonacci, que por su popularidad no
vimos necesario incluir, pero de la que no descartamos futuros
desarrollos. Para el curso siguiente quedarán las recurrentes de tercer
orden.

La comprobación de conjeturas con hoja de cálculo nos parece una
idea que dará bastante juego, porque es una forma sencilla de
internarse en cuestiones profundas. El título es falaz, porque una
conjetura no se puede comprobar con esta herramienta. Sólo se
pretende aclarar conceptos.

Contiene este volumen unas entradas teóricas sobre permutaciones y
ciclos. Con ello no abandonamos la Combinatoria, aunque se percibe
que los contenidos preferidos en estas publicaciones son los números
poligonales y los primos.

Por la edad del autor, cada nuevo volumen conlleva un esfuerzo
mayor. Seguiremos con esta tarea mientras sea divertida y las fuerzas
acompañen. Si se convierte en
interrumpiremos su
publicación.

rutinaria



2





CONTENIDO



Presentación .................................................................................... 2

Contenido ......................................................................................... 3

Seguimos con los poligonales ....................................................... 5

Triangulares de lado par ................................................................ 5

Triangulares y cuadrados con piezas ............................................. 8

Carnaval de cuadrados ................................................................ 18

Igualdad de sumas de cuadrados con un escalón........................ 27

Y seguimos con primos y divisores ............................................. 32

Identidad de cifras con el mdi ...................................................... 32

Identidad con otras partes del número ......................................... 36

Primo y su número de orden ........................................................ 39

Restos en la función primo(n) ...................................................... 44

Números consecutivos, ambos libres de cuadrados .................... 48

Suma de dos números primos consecutivos ................................ 60

Sucesiones recurrentes ................................................................ 69

Recurrencias lineales de segundo orden ..................................... 69

Sucesión de Jacobsthal ............................................................... 75

Números de Pell .......................................................................... 80

Números de Lucas ....................................................................... 86

Soluciones enteras ...................................................................... 92

Comprobación de conjeturas ....................................................... 98

3





Andrica ........................................................................................ 98

Conjetura de Legendre .............................................................. 104

Primo mínimo detrás de un cuadrado ........................................ 107

Conjetura de Brocard y otras cuestiones ................................... 111

Funciones sobre números naturales ......................................... 118

¿De dónde vengo? .................................................................... 118

Tus funciones, disponibles en todas las hojas de cálculo........... 130

Permutaciones y ciclos ............................................................... 138

Grupo simétrico ......................................................................... 138

Descomposición en ciclos .......................................................... 140

Números de Stirling de primera especie. ................................... 146

Permutaciones obtenidas por simulación ................................... 149

Miscelánea ................................................................................... 156

Recogida de datos en tablas de marcado de casillas. ................ 156

Damos vueltas al juego del 2048 ............................................... 161

Distancia de Hamming entre números de igual tipo ................... 169



4


SEGUIMOS CON LO S POLI GON AL ES

Los números poligonales y en especial los triangulares y cuadrados
son fuente continua de cuestiones y curiosidades. Siempre han estado
presentes en volúmenes anteriores y creemos que volverán en los
sucesivos. Algunas cuestiones
implican el uso del sistema de
numeración decimal, lo que resta universalidad a lo estudiado, pero
sus posibilidades hecen que sigamos trabajando con cifras,


T R I A N G U LA R E S DE L A D O P A R


Los números triangulares 3, 10, 21, 36,…son aquellos cuyo número de
orden es par: 3=T(2)=2*3/2; 10=T(4)=4*5/2; 21=T(6)=6*7/2,…Si
aplicamos la expresión algebraica de un número triangular, la de estos
será

T(2n)=2n(2n+1)/2=n(2n+1)=2n2+n

Los podemos representar como formados por filas de triángulos de 3
elementos separados por otros elementos aislados. En la imagen
hemos representado el 36, es decir T(8)



Observa que está formado por 10 triángulos de tres elementos y 6
puntos aislados. Nos sugiere que un número triangular de orden par
equivale a triangular de orden mitad multiplicado por 3 más su
triangular anterior, es decir:

T(2n)=3T(n)+T(n-1)

fácil demostrarlo por

Es
T(4)=3*T(2)+T(1)=3*3+1=10…

inducción: T(2)=3*T(1)+T(0)=3*1+0=3;



5


Probemos con T(2(n+1))=T(2n)+(2n+1)+(2n+2) por definición de
número triangular. Si aceptamos la hipótesis para n, tendremos:

T(2(n+1))=3*T(n)+T(n-1)+(n+1+n+1+n+1)+n=3*T(n)+3*(n+1)+T(n-
1)+n=3*T(n+1)+T(n), luego la hipótesis se cumple para n+1.

La fórmula T(2n)=3T(n)+T(n-1) es válida

Adaptamos una demostración visual contenida en

http://math.berkeley.edu/~rbayer/09su-55/handouts/ProofByPicture-printable.pdf

Así se ve mejor la relación.



En realidad, estos números son los triangulares que no pueden ser
hexagonales. Se sabe que todo hexagonal es triangular, porque su
expresión es H(n)=n(2n-1)=2n(2n-1)/2=T(2n-1), pero el número de
orden del triangular es 2n-1, impar, luego los que no son hexagonales
formarán la sucesión que estamos estudiando: 3, 10, 21, 36,…, que
está contenida en http://oeis.org/A014105

Expresión como resta entre una suma de pares y otra de impares

En la página OEIS enlazada se destacan estas relaciones:

3=4-1

10=6+8-1-3

21=8+10+12-1-3-5

36=10+12+14+16-1-3-5-7



6


No se justifican, y esto es una invitación a que lo hagamos nosotros.
En primer lugar generalizamos. Llamamos a nuestra sucesión TT(n)

TT(n)=T(2n)=SP(2(n+1),n)-SI(1,n)

Con SP(2(n+1),n) deseamos expresar que se toman n números pares
a partir de 2(n+1) y con SI(1,n) que se suman los primeros n impares.
Lo intentamos demostrar por inducción:

TT(n+1)=TT(n)+2n+1+2n+2, como ya sabemos por
anteriores. Si usamos la hipótesis para n queda:

los párrafos

TT(n+1)=2(n+1)+2(n+2)+…+2(2n)-1-3-5-7…- (2n-1)+2n+1+2n+2

Para construir
la nueva suma de pares hay que añadir
2(2n+1)+2(2n+2) y eliminar 2(n+1). La diferencia es 4n+2+4n+4-2n-
2=6n+4, que ha de salir de los nuevos sumandos 2n+1+2n+2=4n+3,
que equivalen a 6n+4-(2n+1), siendo el paréntesis el nuevo impar que
habría que restar, luego la estructura de la fórmula se mantiene y es
correcta.

Usamos el álgebra

TT(n)=T(2n)=n(2n+1)=2n2+n

SP(2(n+1),n)=(2(n+1)+2(2n))*n/2=3n2+n

SI(1,n)=n2 como es sabido.

Por tanto, se verifica la diferencia.

Demostración visual

Ahí te la dejamos para el caso de 36. Analízala e intenta reproducirla
para otros casos:



7


Esta construcción sólo es posible porque el triángulo es de orden par.

Otros desarrollos

Se cumple que TT(n)=T(2n)=3+7+11+15+…(4n-1), es decir, que es la
suma de impares tomados de 4 en 4 a partir de 3. Si sabes verlo, en la
anterior imagen se muestra esa suma con claridad. Puedes justificarlo
algebraicamente:

3+7+11+15+…(4n-1)=(3+4n-1)*n/2=(4n+2)*n/2=n(2n+1)=TT(n)

Este desarrollo se puede escribir así: TT(n)=22-12+42-32+62-52+82-72…,
que es una forma elegante de terminar este tema..



T R I A N G U LA R E S Y C U A D R A D O S C O N P I E Z A S


Quien ha entrado en el mundo de la programación elemental sabe qué
es
la operación de concatenar cadenas (“strings”): situar sus
caracteres uno detrás del otro. Si lo representamos por &, equivaldría a
que “Pablo “&”Pérez”= “Pablo Pérez”. En las hojas de cálculo
disponemos de la función CONCATENAR, que une varios textos de
celdas en uno =CONCATENAR(A12;B22;G1).

Más difícil es concatenar números naturales, de forma que el resultado
sea otro verdadero número en el que cada cifra tenga su valor relativo.
Una forma se basa en esta función CONCATENAR. Para ello debemos
convertir los números en cadenas, con la función TEXTO, después,
concatenarlos, y finalmente, usar la función VALOR para devolverles el
carácter numérico. Tiene un inconveniente, y es que TEXTO ha de ir
acompañado de un formato, y esto lo complica todo. En PARI no existe
es