Mostrar los tags: c
Mostrando del 81 al 90 de 2.861 coincidencias
Se ha buscado por el tag: c
Juego de tetris en pantalla grafica (modo 13), se maneja con las teclas de dirección y escape, para cambiar nivel + y -.
Juego de tetris en pantalla de texto, se maneja con las teclas de dirección y escape.
Para subir o bajar de nivel + y -.

******************************************************************************************
ClaseAula-F896.py
***************************************************************************************
Este ejercicio, sencillo, para aprendizaje y seguimiento de los parámetros: peso,sesgo,costo, en un descenso de gradiente tipo Batch.
***************************************************************************************
Los términos "peso", "sesgo" y "costo" pueden tener diferentes significados dependiendo del contexto en el que se utilicen. Aquí te proporcionaré una breve descripción de cada uno de estos términos en diversos contextos:
Peso (Weight):
En el contexto de la física, el peso se refiere a la fuerza gravitatoria que actúa sobre un objeto debido a la atracción de la gravedad de la Tierra. Se mide en unidades de fuerza, como newtons o libras.
En el aprendizaje automático y la inteligencia artificial, un "peso" se refiere a los coeficientes asociados con las conexiones entre neuronas en una red neuronal. Estos pesos determinan la fuerza y dirección de la influencia de una neurona en otra dentro de la red. Los pesos se ajustan durante el proceso de entrenamiento de la red para que la red pueda aprender y realizar tareas específicas.
Sesgo (Bias):
En el contexto de la estadística y el análisis de datos, el sesgo se refiere a la tendencia sistemática de un conjunto de datos o un modelo estadístico a producir resultados que se desvían de la verdad o de la población real debido a errores sistemáticos en el proceso de recopilación o modelado de datos.
En el aprendizaje automático, el sesgo (bias) es un término que se utiliza para referirse a un valor constante añadido a la salida de una función en una red neuronal. El sesgo permite que la red pueda modelar funciones más complejas, desplazando la función de activación. Es una especie de "ajuste" que ayuda a la red a aprender y generalizar mejor.
Costo (Cost):
En el ámbito empresarial y financiero, el costo se refiere a la cantidad de recursos (dinero, tiempo, esfuerzo, etc.) que se requiere para producir o realizar algo. Puede incluir costos directos e indirectos.
En matemáticas y optimización, el costo es una medida de la cantidad que se desea minimizar o maximizar en un problema. Por ejemplo, en la optimización lineal, se busca minimizar una función de costo sujeta a ciertas restricciones.
En el contexto del aprendizaje automático y la optimización de modelos, el costo es una medida de cuán bien está funcionando un modelo en relación con los datos de entrenamiento y se utiliza para ajustar los parámetros del modelo durante el proceso de entrenamiento. El objetivo es minimizar el costo para que el modelo se ajuste mejor a los datos y pueda realizar predicciones precisas en nuevos datos.
Estos son conceptos que pueden ser ampliamente aplicados en diversos campos y contextos, por lo que su significado puede variar según el contexto específico en el que se utilicen.Hilario Iglesias Martínez.
DescensoGradienteAula-F876.py
El descenso de gradiente tipo "Batch" (también conocido como descenso de gradiente en lotes) es uno de los algoritmos de optimización más utilizados en el aprendizaje automático y la optimización numérica. Este algoritmo se utiliza para minimizar una función de pérdida (también llamada función de costo) al ajustar los parámetros de un modelo de aprendizaje automático. El objetivo principal del descenso de gradiente es encontrar los valores de los parámetros que minimizan la función de pérdida.
Aquí te explico cómo funciona el descenso de gradiente tipo Batch:
Inicialización de parámetros: Se comienza con valores iniciales para los parámetros del modelo. Esto puede ser aleatorio o basado en algún conocimiento previo.
Selección de un lote (batch): En cada iteración del algoritmo, se selecciona un conjunto de ejemplos de entrenamiento del conjunto de datos. Este conjunto de ejemplos se denomina "lote" o "batch". En el descenso de gradiente tipo Batch, se utilizan todos los ejemplos de entrenamiento en cada iteración, es decir, el tamaño del lote es igual al tamaño completo del conjunto de entrenamiento.
Cálculo del gradiente: Para el lote seleccionado, se calcula el gradiente de la función de pérdida con respecto a los parámetros del modelo. El gradiente representa la dirección y la magnitud en la que debe ajustarse cada parámetro para reducir la pérdida.
Actualización de parámetros: Se ajustan los parámetros del modelo en la dirección opuesta al gradiente calculado. Esto se hace multiplicando el gradiente por una tasa de aprendizaje (learning rate) y restando el resultado de los parámetros actuales. La tasa de aprendizaje controla qué tan grande es el paso que se da en cada iteración.
Iteración: Se repiten los pasos 2 a 4 durante un número fijo de iteraciones o hasta que se alcance algún criterio de convergencia (como una pequeña disminución en la función de pérdida o un número máximo de iteraciones).
El proceso se repite hasta que se considera que el modelo ha convergido o alcanzado una solución aceptable.
El descenso de gradiente tipo Batch tiene algunas ventajas, como la convergencia más estable y la posibilidad de aprovechar la paralelización en el hardware moderno. Sin embargo, también puede ser más lento en comparación con variantes más rápidas como el descenso de gradiente estocástico (SGD) o el descenso de gradiente mini-batch, que utilizan subconjuntos más pequeños de los datos en cada iteración. La elección del algoritmo de descenso de gradiente depende de la naturaleza del problema y de las características del conjunto de datos.
****************************************************************************************************************
El Error Cuadrático Medio (MSE, por sus siglas en inglés, Mean Squared Error) es una métrica comúnmente utilizada en estadísticas y machine learning para evaluar el rendimiento de un modelo de regresión o de predicción. MSE se utiliza para medir la calidad de las predicciones de un modelo al calcular la media de los cuadrados de las diferencias entre los valores predichos por el modelo y los valores reales (observados) en un conjunto de datos.
La fórmula del MSE se expresa de la siguiente manera:
MSE = (1/n) Σ(yi - ŷi)²
Donde:
MSE es el Error Cuadrático Medio.
n es el número de muestras en el conjunto de datos.
yi representa el valor real u observado de la muestra i.
ŷi representa el valor predicho por el modelo para la muestra i.
En otras palabras, para calcular el MSE, se toma la diferencia entre el valor predicho y el valor real para cada punto de datos, se eleva al cuadrado, y luego se calcula el promedio de todas estas diferencias al cuadrado.
El MSE es útil para determinar cuán bien se ajusta un modelo de regresión a los datos, y se prefiere minimizarlo. Cuanto menor sea el MSE, mejor será el ajuste del modelo a los datos. Sin embargo, es importante recordar que el MSE puede verse afectado por valores atípicos en los datos y puede no ser la métrica más apropiada en todos los casos. En algunos escenarios, como la detección de valores atípicos, otras métricas como el Error Absoluto Medio (MAE) o el Error Cuadrático Medio Raíz (RMSE) pueden ser más adecuadas.Aula_F-488-8-SepEjercicioBatch.py
[/b]
Hilario Iglesias Martínez.
**********************************************************************************************************
El Descenso de Gradiente Tipo Batch (Batch Gradient Descent en inglés) es un algoritmo de optimización utilizado en el aprendizaje automático y la optimización numérica. Es una variante del Descenso de Gradiente, que es una técnica para ajustar los parámetros de un modelo de manera que minimice una función de costo.
La principal característica del Descenso de Gradiente Tipo Batch es que utiliza todo el conjunto de datos de entrenamiento en cada iteración para calcular el gradiente de la función de costo. Aquí está el proceso básico:
Inicialización: Se comienzan con valores iniciales para los parámetros del modelo.
Cálculo del Gradiente: Se calcula el gradiente de la función de costo con respecto a los parámetros del modelo utilizando todo el conjunto de entrenamiento. El gradiente indica la dirección y la magnitud del cambio necesario para reducir el costo.
Actualización de Parámetros: Se actualizan los parámetros del modelo en la dirección opuesta al gradiente, multiplicados por una tasa de aprendizaje. Esto ajusta los parámetros para minimizar el costo.
Repetición: Los pasos 2 y 3 se repiten para un número determinado de iteraciones o hasta que se cumpla algún criterio de convergencia.
El Descenso de Gradiente Tipo Batch tiene algunas ventajas, como la convergencia a un mínimo global si la función de costo es convexa y una mejor estabilidad en términos de convergencia en comparación con otras variantes del Descenso de Gradiente. Sin embargo, puede ser más lento en términos de tiempo de cómputo cuando se trabaja con conjuntos de datos grandes, ya que requiere el cálculo del gradiente en todo el conjunto de datos en cada iteración.
Existen otras variantes del Descenso de Gradiente, como el Descenso de Gradiente Estocástico (Stochastic Gradient Descent, SGD) y el Descenso de Gradiente Mini-Batch, que combinan características del Descenso de Gradiente Tipo Batch y otras estrategias para lograr un equilibrio entre eficiencia y convergencia. Cada variante tiene sus propias ventajas y se elige según el problema específico y las características de los datos.*****************************************************************************************************
Hilario Iglesias Martínez
ClaseViernes-F543.py
DESCENSO DE GRADIENTE BATCH
*********************************************************************************************************
El "descenso de gradiente tipo Batch" es una técnica de optimización utilizada en el aprendizaje automático y la estadística para ajustar los parámetros de un modelo matemático, como una regresión lineal o una red neuronal, de manera que se minimice una función de costo específica. Es una de las variantes más simples y fundamentales del descenso de gradiente.
Aquí tienes una explicación de cómo funciona el descenso de gradiente tipo Batch:
Inicialización de parámetros: Comienza con un conjunto inicial de parámetros para tu modelo, que generalmente se eligen de manera aleatoria o se establecen en valores iniciales.
Selección de lote (Batch): En el descenso de gradiente tipo Batch, se divide el conjunto de datos de entrenamiento en lotes o subconjuntos más pequeños. Cada lote contiene un número fijo de ejemplos de entrenamiento. Por ejemplo, si tienes 1000 ejemplos de entrenamiento, puedes dividirlos en lotes de 32 ejemplos cada uno.
Cálculo del gradiente: Para cada lote, calculas el gradiente de la función de costo con respecto a los parámetros del modelo. El gradiente es una medida de cómo cambia la función de costo cuando se hacen pequeños ajustes en los parámetros. Indica la dirección en la que debes moverte para minimizar la función de costo.
Actualización de parámetros: Después de calcular el gradiente para cada lote, promedias los gradientes de todos los lotes y utilizas ese gradiente promedio para actualizar los parámetros del modelo. Esto se hace multiplicando el gradiente promedio por una tasa de aprendizaje (learning rate) y restando ese valor de los parámetros actuales. El learning rate controla el tamaño de los pasos que das en la dirección del gradiente.
Repetición: Los pasos 2-4 se repiten varias veces (llamadas épocas) a través de todo el conjunto de datos de entrenamiento. Cada época consiste en procesar todos los lotes y ajustar los parámetros del modelo.
Convergencia: El proceso de ajuste de parámetros continúa hasta que se alcanza un criterio de convergencia, que generalmente se establece en función de la precisión deseada o el número de épocas.
El descenso de gradiente tipo Batch es eficiente en términos de cómputo, ya que utiliza todos los datos de entrenamiento en cada paso de actualización de parámetros. Sin embargo, puede ser lento en conjuntos de datos grandes, y su convergencia puede ser más lenta en comparación con otras variantes del descenso de gradiente, como el descenso de gradiente estocástico (SGD) o el mini-batch SGD.
En resumen, el descenso de gradiente tipo Batch es una técnica de optimización que ajusta los parámetros de un modelo mediante el cálculo y la actualización de gradientes en lotes de datos de entrenamiento, con el objetivo de minimizar una función de costo. Es una parte fundamental en la optimización de modelos de aprendizaje automático.
*********************************************************************************************************
Ejecucion.
Bajo consola de Linux.
python3 ClaseViernes-F543.py[
b]"""
Hilario Iglesias Martinez.
*****************************************************
seno.py
********************************************************
Descenso de gradiente en una función seno.
----------------------------------------------------------
Función Seno (sin(x)): La función seno es una función trigonométrica
que toma un ángulo como entrada y devuelve la relación entre
la longitud del cateto opuesto a ese ángulo y la longitud de
la hipotenusa en un triángulo rectángulo. En términos más simples,
el valor del seno de un ángulo en un triángulo rectángulo es igual
a la longitud del lado opuesto dividido por la longitud de la hipotenusa.
En el contexto de funciones reales, la función seno asigna un valor
real a un ángulo en radianes. Su gráfica oscila entre -1 y 1,
creando una forma ondulante suave que se repite cada 2π radianes.
--------------------------------------------------------------------[/b]
EJECUCION BAJO CONSOLA LINUX.
python3 seno.py
*********************************************************
Hilario Iglesias Martínez
**********************************************************
La función sigmoide es una función matemática que toma
cualquier número real como entrada y la transforma en
un valor en el rango de 0 a 1. Su forma característica
es una curva en forma de "S".
La función sigmoide es comúnmente utilizada en diversos campos,
como la biología, la psicología y el aprendizaje automático,
especialmente en las redes neuronales.
Forma:
f(x)=1 / (1 + e**(-x))
Derivada:
e**(-x) / (1 + e**(-x))**2
La función sigmoide toma valores positivos y negativos de
x y los mapea en el rango (0, 1), de modo que valores grandes de
x resultarán en valores cercanos a 1, y valores pequeños o negativos de
x resultarán en valores cercanos a 0.
Programa realizado bajo linux
Plataforma Ubuntu 20.04.6 LTS.
Editado con Sublime Text.
Ejecucion en consola linux.
python3 SigmoideWeb.py
Tambien se puede editar y ejecutar en Google Colab."""
**************************
De parvis grandis acervus erit
**************************
NumeroEuler.py
**************************
Hilario Iglesias Martínez.
**************************
Ecuacion para datos de entrada:
f(x,z)=(x**2/4)+(e*z)
e=Número de Euler.
2.71828
Valores de entrada [5,12] La salida real debería ser=38.86936
Realizado bajo plataforma Linux.
Ubuntu 20.04.6 LTS.
Google Colaboratory.
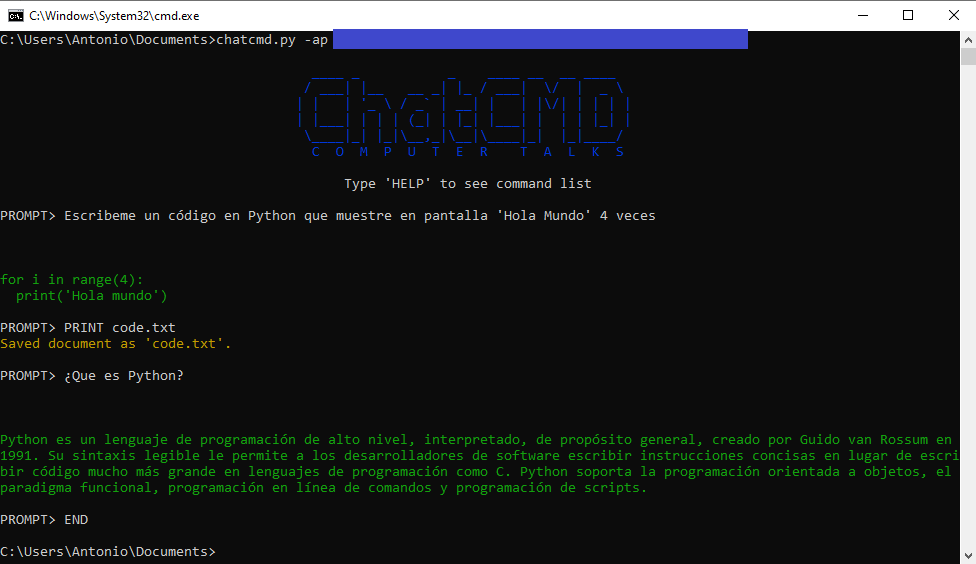
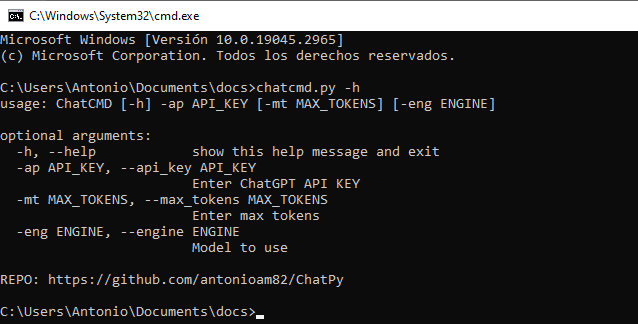
"""Programa para usar ChatGPT dese la terminal. Al iniciarlo se requiere introducir la Api-Key del usuario.
PARA CUALQUIER DUDA U OBSERVACIÓN, USEN LA SECCIÓN DE COMENTARIOS.





 (7)
(7)



